Очевидно, если две плоскости взаимно перпендикулярны, мы должны использовать даную нам аксиому 4, В которой говорится что Если 2 плоскости имеют общую точку, то они пересекаются по прямой. Нам дано что угол пересечения равен 90 градусам, что дает нам понять что треугольники будут задействованы. Проведем отрезки из точки А равные 20 и 21 см. Оттуда мы их соединим, и продлим их. Получим 2 квадрата гипотенузы умноженные на 4. После чего нужно использовать формулу радиуса окружности вокруг треугольника за площадью. (Герона) После этого спокойно говорим что за Теоремой 2.2 2 прямые лежать в 1 плоскости. Так как они пересекают плоскость (пускай альфа) то они лежат в этой площине за 3 аксиомой.Из этого выходит что угол пересечаения дает нам использовать все теоремы планиметрии. ТАкие как теорема Пифагора или среднего значения. Из чего выплывает ответ : 20.5 см!
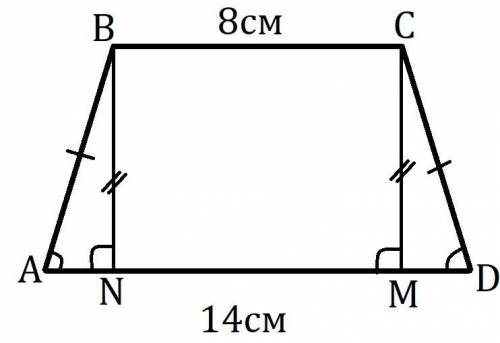
Дана трапеция ABCD, BC║AD, AB=CD, BC=8см, AD=14см, S(ABCD)=44см².
Найти P(ABCD).
Пусть CM⊥AD, BN⊥AD и M,N∈AD.
Площадь трапеции равна произведению средней линии и высоты опущенной на основание.
S(ABCD) =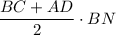 
= BN·(8см+14см):2 = BN·11см = 44см²
BN = 44:11 см = 4см
ΔABN = ΔDCM по гипотенузе и острому углу (AB=DC и ∠BAN=∠CDM т.к. трапеция равнобедренная), поэтому AN=MD
NBCM - прямоугольник, поэтому NM=BC=8см
AN = (AD-NM):2 = (14см-8см):2 = 3см
В прямоугольном ΔABN (∠N=90°): BN=4см и AN=3см, по Египетскому треугольнику AB=5см.
CD=AB=5см
P(ABCD) = AB+BC+CD+AD = 5см+8см+5см+14см = 32см
ответ: 32см.
Расстояние L равно гипотенузе треугольника с катетами 20 и 21 см.
L = √(20² + 21²) = √(400 + 441) = √841 = 29 см.