A(-3; 4) b(7; 2) найти точку m лежащую на оси ординат и равноудаленные от a и b

Question

Геометрия: A(-3; 4) b(7; 2) найти точку m лежащую на оси ординат и равноудаленные от a и b

prvvk · Accepted Answer

Рассмотрим прямоугольный треугольник SOA в нём радиус описанной окружности основания равен: OA=AB=18. По теореме Пифагора найдем

высоту пирамиды SO.

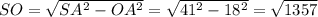
$SO=\sqrt{SA^2-OA^2}=\sqrt{41^2-18^2} =\sqrt{1357}$

Теперь рассмотрим прямоугольный треугольник SOK. SK - апофема пирамиды, OK - радиус вписанной окружности основания.

OK = AB√3/2 = 9√3

Тогда 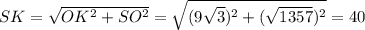$SK=\sqrt{OK^2+SO^2}=\sqrt{(9\sqrt{3})^2+(\sqrt{1357})^2}= 40$

Площадь одной грани (треугольник SBA): S = AB*SK/2 = 18*40/2 = 360

Площадь боковой поверхности пирамиды- это сумма всех площадей грани . В шестиугольной пирамиде граней 6, значит площадь боковой поверхности пирамиды равна: Sбок = 6*360 = 2160

ответ: 2160.

Сторона основания правильной шестиугольной пирамиды 18, боковое ребро 41. найти площадь боковой пове

MOGZ ответил