Дано:
ΔABC - равнобедренный
BE - высота; AB=BC
AC= 2√23
AB=12
Найти: BE=?
Решение: 1) AB=BC= 12, BE является и выстой, и биссектрисой, и медианой (по свойству равнобедр. треугольников) => AE=EC= (2√23)/2=√23
2) BE - катет для прямоугольных треугольников ABE и CBE (т.к. высота образует угол 90 градусов) => по Т Пифагора BE= √(AB²- AE²)= √(144 -23)= √121= 11
ответ: BE = 11
Объяснение: - - - - - - - задание N 1 - - - - - - -
- Центр окружности, вписанной в тупоугольный треугольник ,находится вне треугольник ← (неверно)
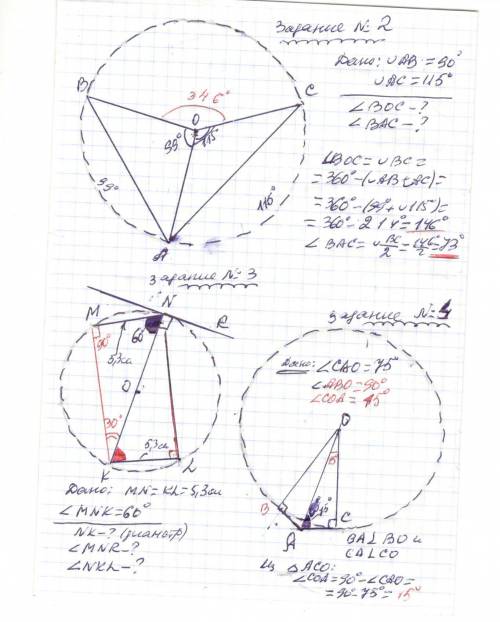
- - - - - - - задание N 2 - - - - - - -
◡ BC = 360° -(◡AB + ◡AC) =360° -( 99°+ 115°) =360° -214° = 146°
∠BOC = ◡ BC = 146° как центральный угол
∠BAC = ◡ BC/2 = 146°/2 = 73° как вписанный угол
- - - - - - - задание N 3 - - - - - - -
KN ⊥ NR ( NR касательная окружности в точке касания N )
NK диаметр ⇒ ∠NMK = 90° (вписанный угол опирающий на диаметр)
В прямоугольном треугольнике NMK :
∠MKN = 90° - ∠MNK = 90° - 60° = 30°
MK =NK/2 ( как катет против угла 30° ) ⇒ NK =2*MK =2*5,3 см =10,6 см
∠MNR = ∠MNK+∠KNR =60°+90° =150° .
ΔKLN = ΔNMK ( по гипотенузе и катету)
следовательно ∠NKL = ∠ KNM = 60° .
* * * * NMKL прямоугольник * * *
- - - - - - - задание N 4 - - - - - - -
BA ⊥ BO , CA ⊥ cO
∠ABO = 90° , ∠ACO = 90°
Из ΔACO: ∠COA = 90° - ∠CAO = 90° - 75° =15° рис. см приложение
ВЕ^2=АВ^2-АЕ^2
Найдём сторону АЕ, так как треугольник РАВНОБЕДРЕННЫЙ, то сторона АЕ = АС/2
Находим теперь сторону ВЕ
ответ: ВЕ=11