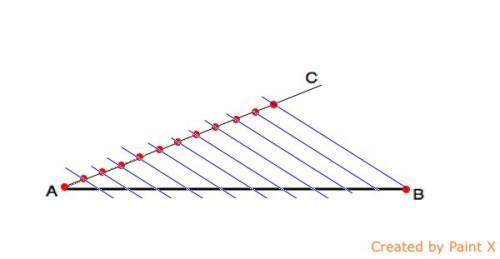
Общепринято мнение, что египетский треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов египетскими землемерами и архитекторами, например, при построении пирамид.
Для построения прямого угла использовался шнур или верёвка, разделённая отметками (узлами) на 12 (3+4+5) частей: треугольник, построенный натяжением такого шнура, с весьма высокой точностью оказывался прямоугольным и сами шнуры-катеты являлись направляющими для кладки прямого угла сооружения.
Судя по всему, именно попытка обобщения отношения квадратов, характерного для египетского треугольника, на любые прямоугольные треугольники и привела Пифагора к доказательству знаменитой теоремы.
Для двух концентрических окружностей:
r1-r2=h
P1-P2=1
P1-P2 =2п(r1-r2) <=> 2пh=1 <=> h= 1/2п (км)
Прямые (параллельные) участки не влияют на разность периметров. Суммарный поворот составляет 360 (мы возвращаемся в исходное положение).
x1, x2, y1, y2 ... - радиусы поворота
x1-x2 = y1-y2 ... =h
a_x, a_y ... - соответствующие углы поворота
a_x + a_y ... =360
P1-P2 = пx1*a_x/180 - пx2*a_x/180 + пy1*a_y/180 - пy2*a_y/180 ... <=>
hпa_x/180 + hпa_y/180 ... =1 <=>
hп (a_x + a_y ...)/180 =1 <=>
hп 360/180 =1 <=>
h= 1/2п (км) ~159 м