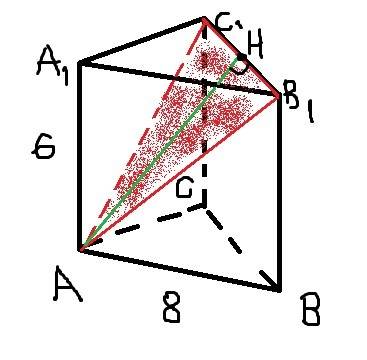
ВСС₁В₁ прямоугольник
ΔАВС - равнобедренный
АВ = АС = √746 ≈ 27,3 см
Объяснение:
Если в четырехугольнике две противоположные стороны параллельны и равны, то это параллелограмм.
Если в параллелограмме есть прямой угол, то это прямоугольник.
ВВ₁ ║ СС₁ как перпендикуляры к одной плоскости,
ВВ₁ = СС₁ = 11 см по условию, значит
ВСС₁В₁ прямоугольник.
ΔАВ₁В = ΔАС₁С по двум катетам (∠АВ₁В = ∠АС₁С = 90°, ВВ₁ = СС₁ и АВ₁ = АС₁), значит АВ = АС, тогда
ΔАВС - равнобедренный.
ΔАВВ₁: ∠АВ₁В = 90°, по теореме Пифагора
АВ = √(АВ₁² + ВВ₁²) = √(25² + 11²) = √(625 + 121) = √746 см
АВ = АС = √746 ≈ 27,3 см
Пусть дан четырёхугольник АВСD. Точка К - середина АВ, т.М - середина ВС, N и Т - середины СD и DA соответсвенно. По условию КN=ТМ. Проведем диагонали АС и ВD. Соединим середины сторон треугольников АВС, ВСD, CDA и DAB. В треугольниках АВС и АDC средние линии параллельны и равны половине диагонали АС исходного четырехугольника.⇒ КМ параллельна и равна ТN. Аналогично доказывается КТ=МN. Противоположные стороны КМNТ параллельны и равны. КМNТ - параллелограмм с равными диагоналями ( КN=МТ по условию), т.е. КМNТ - прямоугольник. А раз стороны КМNТ пересекаются под прямым углом, то и диагонали четырехугольника АВСD, которым они параллельны, также пересекаются под прямым углом, ч.т.д.