Объяснение:
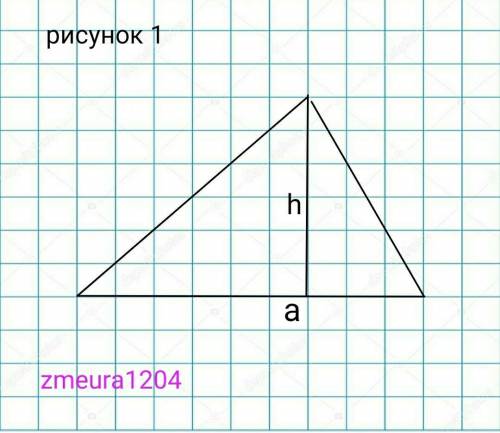
1) рисунок 1.
Дано:
Треугольник
а=48см
S=72cм²
h=?
Решение
S=1/2*a*h, где а- сторона треугольника, h- высота опущенная на сторону а.
h=2*S/a=2*72/48=3 см
ответ: 3см.
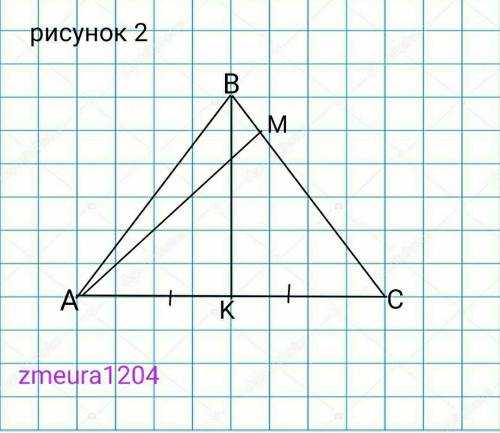
2) рисунок 2
Дано
∆АВС- равнобедренный
АВ=ВС
АС=20см
ВК=24см
АС=?
Решение
ВК- высота, медиана и биссектрисса, равнобедренного треугольника ∆АВС.
АК=КС
КС=АС:2=20:2=10см.
∆ВКС- прямоугольный треугольник.
По теореме Пифагора
ВС=√(ВК²+КС²)=√(24²+10²)=26см.
S=1/2*BK*AC=1/2*24*20=240 см²
S=1/2*AM*BC
AM=2*S/BC=2*240/26=480/26=
=18цел6/13 см
ответ: АМ=18цел6/13 см
Дано: трапеция АВСД, где ВС – меньшее основание. АВ=ВС=СД. Из т.В опустили высоту ВЕ к стороне АД. Точка О – пересечение ВЕ и АС. ВО=10, ОЕ=8.
1) 1) Пусть ВС=х, тогда АВ=х. Из треугольника АВЕ: АЕ^2=AB^2-BE^2=x^2-(10+8)^2=x^2-324
2) 2) Треугольники АОЕ и ВОС подобны по 2-м углам (углы АОЕ и ВОС равны как вертикальные; углы ОАЕ и ОСВ равны как накрест лежащие при 2-х параллельных прямых), тогда АЕ:ВС=ОЕ:ОВ. Отсюда АЕ=ВС*ОЕ/ОВ=х*8/10. Значит АЕ^2=x^2*64/100
3) 3) Подставим уравнение из п.2 в п.1: x^2-324= x^2*64/100. Отсюда х=30
4) 4) Тогда АЕ^2=30^2-324=576. Отсюда АЕ=24
5) 5) АД=ВС+2*АЕ=30+2*24=78
6) 6) S=1/2*(ВС+АД)*ВЕ=1/2*(30+78)*18=972
итак по началу рассмотрим треугольник AOD AD=BC=16
AC=BD КАК ДИАГОНАЛИ они точкой пересечения делятся пополам, AO=12=OD
PAOD=16+12+12=30