Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.

Формулы определения координат вектора заданного координатами его начальной и конечной точки
Формула определения координат вектора для плоских задач
В случае плоской задачи вектор AB заданный координатами точек A(Ax ; Ay) и B(Bx ; By) можно найти воспользовавшись следующей формулой
AB = {Bx - Ax ; By - Ay}
Формула определения координат вектора для пространственных задач
В случае пространственной задачи вектор AB заданный координатами точек A(Ax ; Ay ; Az) и B(Bx ; By ; Bz) можно найти воспользовавшись следующей формулой
AB = {Bx - Ax ; By - Ay ; Bz - Az}
Формула определения координат вектора для n -мерного пространства
В случае n-мерного пространства вектор AB заданный координатами точек A(A1 ; A2 ; ... ; An) и B(B1 ; B2 ; ... ; Bn) можно найти воспользовавшись следующей формулой
AB = {B1 - A1 ; B2 - A2 ; ... ; Bn - An}
Примеры задач связанных с определением координат вектора по двум точкам
Примеры для плоских задач
Пример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).
Решение: AB = {3 - 1; 1 - 4} = {2; -3}.
Пример 2. Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).
ABx = Bx - Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8
ABy = By - Ay => By = ABy + Ay => By = 1 + (-4) = -3
ответ: B(8; -3).
Пример 3. Найти координаты точки A вектора AB = {5; 1}, если координаты точки B(3; -4).
ABx = Bx - Ax => Ax = Bx - ABx => Ax = 3 - 5 = -2
ABy = By - Ay => Ay = By - ABy => Ay = -4 - 1 = -5
ответ: A(-2; -5).
Примеры для пространственных задач
Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).
Решение: AB = {3 - 1; 1 - 4; 1 - 5} = {2; -3; -4}.
Пример 5. Найти координаты точки B вектора AB = {5; 1; 2}, если координаты точки A(3; -4; 3).
ABx = Bx - Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8
ABy = By - Ay => By = ABy + Ay => By = 1 + (-4) = -3
ABz = Bz - Az => Bz = ABz + Az => Bz = 2 + 3 = 5
ответ: B(8; -3; 5).
Пример 6. Найти координаты точки A вектора AB = {5; 1; 4}, если координаты точки B(3; -4; 1).
ABx = Bx - Ax => Ax = Bx - ABx => Ax = 3 - 5 = -2
ABy = By - Ay => Ay = By - ABy => Ay = -4 - 1 = -5
ABz = Bz - Az => Az = Bz - ABz => Az = 1 - 4 = -3
ответ: A(-2; -5; -3).
Примеры для n -мерного пространства
Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).
Решение: AB = {3 - 1; 0 - 4; 1 - 5; -2 - 5; 5 - (-3)} = {2; -4; -4; -7; 8}.
Пример 8. Найти координаты точки B вектора AB = {5; 1; 2; 1}, если координаты точки A(3; -4; 3; 2).
AB1 = B1 - A1 => B1 = AB1 + A1 => B1 = 5 + 3 = 8
AB2 = B2 - A2 => B2 = AB2 + A2 => B2 = 1 + (-4) = -3
AB3 = B3 - A3 => B3 = AB3 + A3 => B3 = 2 + 3 = 5
AB4 = B4 - A4 => B4 = AB4 + A4 => B4 = 1 + 2 = 3
ответ: B(8; -3; 5; 3).
Пример 9. Найти координаты точки A вектора AB = {5; 1; 4; 5}, если координаты точки B(3; -4; 1; 8).
AB1 = B1 - A1 => A1 = B1 - AB1 => A1 = 3 - 5 = -2
AB2 = B2 - A2 => A2 = B2 - AB2 => A2 = -4 - 1 = -5
AB3 = B3 - A3 => A3 = B3 - AB3 => A3 = 1 - 4 = -3
AB4 = B4 - A4 => A4 = B4 - AB4 => A4 = 8 - 5 = 3
ответ: A(-2; -5; -3; 3).
Объяснение:
100%
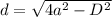
![D= \sqrt{4a^2-d^2} [/tex [tex]6= \sqrt{4a^2-8^2}](/tpl/images/0722/6698/73107.png)
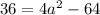
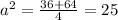
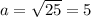
дано: треугольникabc=треугольникpqr
ab= 5см,bc= 6см,ac=7см решение: треугольники равны,равны все и соответсвующие стороны и углы. pq = ab = 5см,qr=bc=6см,pr = ac = 7см ответ: pq = 5см,qr = 6см,pr=7см.