1) отложить отрезок, равный данному(данной стороне)(базовая задача на построение)
2) от одного окнца отрезка отложить угол равный одному из даных углов(прилегающих к стороне) (базовая задача на построение)
3) от другого конца отложить угол равный другому углу(прилегающему к стороне треугольника)(базовая задача на построение)
стороны этих построенных углов пересекутся в точке третьей верине треугольника, две другие концы отрезка
примечание углы нужно откладывать в одной итой же полуплоскости от отрезка(пряма, что содержит отрезок делит плоскость на две полуплоскости - верхнююи нижнюю, углы нужно откладывать в любой, но одной и той же дяля обоих углов)
Дано :
параллелограмм NPKA
<ANK = 45°
<KNP = 65°
Найти:
<А, <К, <Р, <N, <NKA, <NKP = ?
<N = <ANK + <KNP = 45° + 65° = 110°
<N = <K = 110° (св-во параллелограмма - противоположные углы равны)
<А = 180° - <К = 180° - 110° = 70° (свойство параллелограмма - углы, прилежащие к любой стороне, в сумме равны 180°)
<Р = <А = 70° (св-во параллелограмма - противоположные углы равны)
<NKA = <KNP = 65° (н.л. при NP//AK и секущей NK)
<NKP = <K - <NKA = 110° - 65° = 45°
ответ: <А = <Р = 70° ; <К = <N = 110° ; <NKA = 65° ; <NKP = 45°
BC = 5;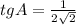
Геометрический смысл тангенса:
tgA = BC/AC => AC = BC/tgA (1)
Теорема Пифагора:
AB^2 = AC^2+BC^2 (2)
Подставим (1) в (2) и решим это уравнение:
Подставим известные: