Построение с циркуля и линейки.
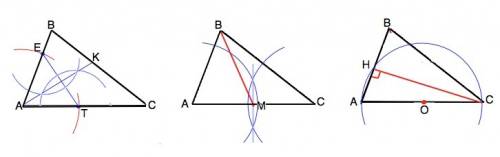
а) биссектрисы АК.
Применим известный метод построения срединного перпендикуляра ( деления отрезка пополам).
Из вершины А,как из центра, на сторонах АВ и АС отмечаем циркулем равные отрезки АЕ и АТ.
Из т.т. Е и Т как из центров проводим полуокружности. Соединим точки их пересечения прямой. Они пройдут через А и пересекут ВС в точке К.
АК - биссектриса, т.к. треугольник АЕТ - равнобедренный по построению, АК - срединный перпендикуляр, для равнобедренного треугольника он медиана и биссектриса.
б) медианы ВМ
Для построения медианы ВМ по вышеописанному методу находим середину АС и соединяем с вершиной В.
в) высоты СН.
Для построения высоты находим точку О - середину АС. Из нее как из центра проводим окружность радиусом АО. АО=ОС, АС - диаметр. Точка пересечения окружности с АВ - основание высоты СН, т.к. вписанный угол АНС опирается на диаметр и равен 90°.
Высота построена.
1. 15 см²
2. 8 см²
Объяснение:
1. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними
S = (6*10* ½) / 2= 15 см²
2. Острый угол параллелограмма равен 180° -150° = 30°
Разделим параллелограмм на два треугольника соединив вершины тупых углов, высотам которых будут высоты параллелограмма
Основание к которому проведена высота 4см равна 3*sin30=3/2=1,5
Основание к которому проведена высота 3см равна 4*sin30=4/2=2
S=½* 4* 1,5 + ½* 3* 2= 3+5=8 см²
Но это опять же при условии что угол не 300 градусов, а 30.