Рисунок - во вложении.
Т.к. E и F - внутренние точки отрезка АВ, и по условию АЕ=BF, то
для EB=AB-AE и для AF=AB-BF следует, что EB=AF.
Рассмотрим прямоугольные ΔADF и ΔВСЕ. У них: 1) АD=BC (противолежащие стороны прямоугольника); 2) AF=EB (по доказанному выше). Значит, ΔADF = ΔВСЕ по двум катетам.
Из равенства этих треугольников следует, что ∠DFA=∠СЕВ. Отсюда, ΔEGF - равнобедренный с основанием EF, тогда GF=GE. Доказан пункт Б).
Т.к. АВСD - прямоугольник, то АВ║CD. Тогда ∠EFG=∠GDC(как накрестлежащие при секущей FD) и ∠FEG=∠GCD (как накрестлежащие при секущей ЕС). Отсюда, ΔDGС - равнобедренный с основанием DC, тогда DG=GC. Доказан пункт A).
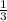BK=
. Значит, DK=2NK=2. Считаем площадь равнобедренного ADC=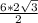
=6. Получаем, наконец, площадь полной поверхности: 3+3*6=21 (площадь основания плюс площади трех боковых граней).
. И наконец, V=9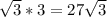
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Это если коротко. Но решением мы должны это доказать. Проведите высоту через точку пересечения диагоналей. Эта точка делит высоту на два отрезка - это высоты двух подобных треугольников. Обратите внимание они прямоугольные и равнобедренные. Поэтому если высота верхнего маленького треугольника х, то высота нижнего, большого треугольника, 54-х. А так как треугольники равнобедренные, то верхнее основания 2х, а нижнее 108-2х. Средняя линия это полусумма основ, отсюда следует (2х+108-2х)/2=108/2=54