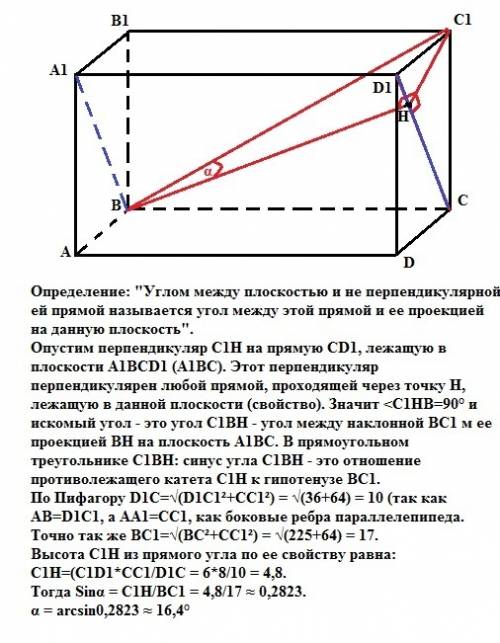
Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.
Высота С1Н из прямого угла по ее свойству равна:
С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.
Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.
α = arcsin0,2823 ≈ 16,4°.
Формула объема параллелепипеда V=S•h, где Ѕ - площадь основания параллелепипеда, h - его высота. В прямом параллелепипеде боковые ребра перпендикулярны основанию, поэтому высота равна его боковому ребру.
Диагональ основания делит его на два равных треугольника, площадь каждого, найденная по формуле Герона, равна 36 ед. площади. Площадь основания 2•36=72.
Площадь всей поверхности состоит из суммы площади боковой поверхности и площади двух оснований. Площадь боковой поверхности находим вычитанием из площади полной поверхности площади двух оснований. Ѕ(бок)=334-2•72=190.
S(бок)=Р•h. Периметр основания Р=2•(10+9)=38 ⇒ h=190:38=5 Искомый объём V=72•5=360 ( ед. объема).

Вот так получается