ответ: 8 сторон
Объяснение: Сумма внешних углов выпуклого многоугольника ( любого) равна 360°.
Сумма внутренних углов данного многоугольника по условию
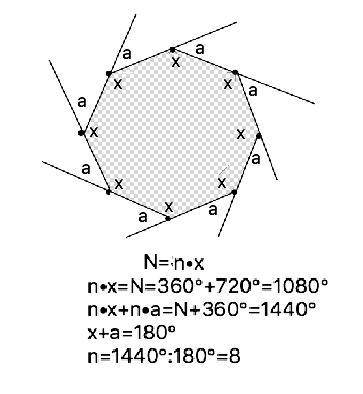
360°+720°=1080°.
Если N- сумма внутренних углов, то их количество находят по формуле
N=180°•(n-2), где n - число сторон многоугольника.
1080°=180°•n -360° , откуда
n=1448°:180°=8
Иногда удобнее применять другой с тем же результатом).
Сколько бы ни было сторон у выпуклого многоугольника, каждый внутренний угол с одним внешним при той же вершине составляет в сумме 180° ( развернутый угол).
Сумма внутренних (1080°) и внешних ( 360°) углов данного многоугольника = 1080°+360°= 1440°
Делим на величину развёрнутого угла:
1440°:180°=8 ( сторон),
FG = 8 - средняя линия
NE = 3; BN=NC; AE=ED
Продлить стороны AB и DC ⇒ получился ΔBMC
∠MBC = 180° - ∠ABC = 180°-160° = 20°
∠BCM = 180° - ∠BCD = 180°-110° = 70°
∠BMC = 180° - ∠MBC - ∠BCM = 180° - 20° - 70° = 90° ⇒
ΔBMC - прямоугольный ⇒
медиана MN равна половине гипотенузы BC
MN = BN = NC = X ⇒ ΔMNC - равнобедренный
BC║FG - средняя линия трапеции ⇒
ΔKMG подобен ΔNMC по двум соответственным углам ⇒
MK = KG ⇒ X + ЕN/2 = FG/2
X = 4 - 1,5 = 2,5
BC = 2X = 5
Средняя линия FG = (BC + AD)/2 = 8
BC + AD = 16; AD = 16 - 5 = 11
Основания трапеции равны 5 и 11