1. полупериметр 50/2=25, одна из сторон АВ=СD=10cм⇒две другие BC=AD=25-10=15/см/
ответ 10 см, 15 см.
2. задача задана некорректно, если угол А равен 36° , то угол В равен 90°, т.к. угол С равен 117°, но угол С равен не 117°, а 90°, и тогда угол D равен 117°. Если бы в задаче была трапеция АВDС, то корректность условия была бы налицо.
Если бы не было именованных сторон, т.е. указали бы два угла острый и тупой, но даже если бы выполнялись эти все условия. задача все равно некорректна, т.к. сумма углов четырехугольника равна 360°, два угла прямых, это 180°, а сумма двух других 117°+36°≠180°
3. периметр - это сумма всех сторон. у квадрата они равны. поэтому периметр равен 4*4=16/см/
4. Т.к. ∠В=60°, то в ΔАВС углы А и С тоже по 60°, ΔАВС- равносторонний. т.е. сторона ромба равна диагонали АС, 10.5см, а его периметр 10.5*4=42/см/
5. О- точка пересечения диагоналей. т.к. диагонали параллелограмма, пересекаясь, делятся точкой пересечения пополам, поэтому противолежащие вершины параллелограмма находятся на одинаковом расстоянии от точки пересечения диагоналей, а потому О- центр симметрии. Доказано.
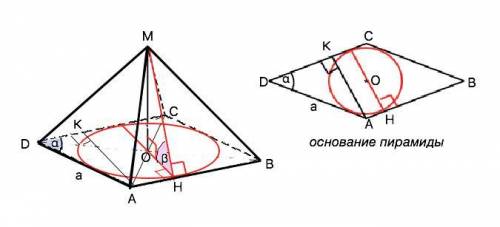
ответ: V=a³•sin²α•tgβ/6
Объяснение - очень подробно:
Формула объема пирамиды V=S•h/3, где S – площадь основания пирамиды, h - её высота.
Стороны ромба равны. По условию боковые грани наклонены к плоскости основания под углом β.
Если боковые грани пирамиды наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проецируется в центр этой окружности.
Центр окружности, вписанной в ромб – точка пересечения его диагоналей, а расстояние от него до сторон равно радиусу вписанной окружности.
Высота пирамиды, радиус вписанной окружности и высота боковой грани образуют прямоугольный треугольник, при этом высота боковой грани и радиус вписанной окружности образуют линейный угол между основанием и боковой гранью, т.к. по т. о 3-х перпендикулярах перпендикулярны стороне ромба (ребру двугранного угла) в одной точке.
Диаметр окружности, вписанной в ромб, перпендикулярен его сторонам, параллелен высоте ромба и равен ей. На рисунке приложения АК = высота ромба. АК=АD•sinα=a•sinα ⇒ HO=r=a•sinα•1/2. Из прямоугольного ∆ МОН высота пирамиды МО=ОН•tgβ=(a•sinα•1/2)tgβ
S(ABCD)=AD•CD•sinα=a²•sinα
V=a²•sinα•(a•sinα•1/2)tgβ/3=a³•sin²α•tgβ/6
Извини не знаю как построить "серединный перпендикуляр на катеты прилежащий к углу"
Остальное решение в файле.