Дано :
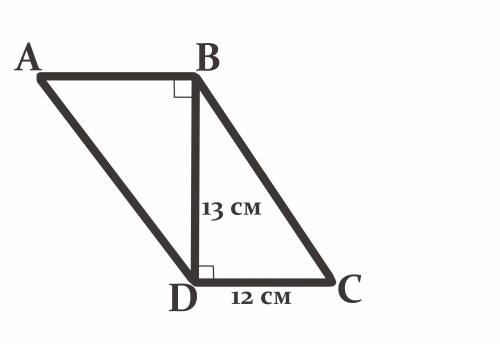
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
1)Пусть х = 1: Пусть х = 4:
f(1) + 2f(4) = -4 f(4) + 2f(1) = 11/4
Решаем систему уравнений:
f(4) = 11/4 - 2f(1)
f(1) -4f(1) + 22/4 = -4 3f(1) = 38/4 f(1) = 19/6
ответ: 19/6.
2) При x<5:
y = -x^2 + 5x -1
парабола с вершиной в т( 2,5; 5,25) ветвями вниз.
При x>=5:
y = x^2 - 5x -1
Парабола с вершиной в т.(2,5; -7,25) ветвями вверх(рисуем кусок правой ветви)
Проверяем значения на краях отрезка и сравниваем их с вершиной параболы, которая тоже входит в указанный отрезок.
У(-2) = -4-10-1 = -15
у(2,5) = 5,25
у(6) = 5
Итак у прин [-15; 5,25]
С И д ннет