100 ! если основанием пирамиды есть треугольник со сторонами 4, 5 и 7см, а высота пирамиды равна наибольшей высоте основания, то чему равен объем пирамиды? решение обязательно с рисунком

👇

Ответ:

bulochka228

14.02.2023

Если основанием пирамиды есть треугольник со сторонами 4, 5 и 7см, а высота пирамиды равна наибольшей высоте основания, то чему равен объем пирамиды?

РЕШЕНИЕ:

• Рассмотрим тр. АВС:
По формуле Герона найдём площадь треугольника АВС:

$s = \sqrt{p(p - a)(p - b)(p - c)} \\$
где р = ( а + b + c ) / 2 - полупериметр, а, b и с - стороны треугольника

$s = \sqrt{8 \times (8 - 4)(8 - 5)(8 - 7)} = \sqrt{8 \times 4 \times 3 \times 1} = \\ = \sqrt{4 \times4 \times 6} = 4 \sqrt{6} \\$
• Площадь треугольника АВС равна:
S abc = ( 1/2 ) • AC • h1
4V6 = ( 1/2 ) • 4 • h1
h1 = 2V6

• S abc = ( 1/2 ) • AB • h2
4V6 = ( 1/2 ) • 5 • h2
h2 = 8V6 / 5

• S abc = ( 1/2 ) • BC • h3
4V6 = ( 1/2 ) • 7 • h3
h3 = 8V6 / 7

Наибольшая высота треугольника АВС равна 2V6
Значит, ED = 2V6

• Обьём пирамиды ЕАВС равен:
V = ( 1/3 ) • S abc • ED = ( 1/3 ) • 4V6 • 2V6 = 2 • 8 = 16

ОТВЕТ: 16

100 ! если основанием пирамиды есть треугольник со сторонами 4, 5 и 7см, а высота пирамиды равна наи

100 ! если основанием пирамиды есть треугольник со сторонами 4, 5 и 7см, а высота пирамиды равна наи

4,8(83 оценок)

Открыть все ответы

Ответ:

sooooooyeees

14.02.2023

Рух - відображення площині на себе, при якому відстані між точками площини зберігаються. Приклади руху: осьова симетрія, центральна симетрія, паралельний перенос. Властивості руху: відрізок переходить в відрізок, кут переходить в рівний йому кут, окружність переходить в окружність того ж радіуса і т. П.Мал. 1. Нехай є деяка виділена точка Про площині. Крім того, розглянемо довільну точку М тій же площині. Поворотом (позначення -) щодо точки О, званої центром повороту на Ðα (кут повороту) називається таке відображення площині на себе, при якому будь-яка точка М площині переходить в таку точку М1 тій же площині, що ОМ = ОМ1 і, крім того, ÐМОМ1 = α (Рис. 1). Доведемо, що поворот є рухом. Доказ (Рис. 2).Розглянемо точки М і N площині, що переходять при повороті відповідно в точки М1 і N1 тій же площині. Розглянемо трикутники ОМN і ОМ1N1. У цих трикутниках ОМ = ОМ1 і ОN = ОN1. ÐМОN = α - ÐМОN1; ÐМ1ОN1 = α - ÐМОN1, отже, ÐМОN = ÐМ1ОN1. Таким чином, зазначені трикутники рівні за двома сторонами і кутом між ними. Звідси випливає рівність відрізків МN = М1N1. Оскільки точки М і N вибиралися нами довільно, можна стверджувати, що при повороті довжини відрізків зберігаються. Теорема доведена. Нам необхідно навчитися використовувати розглянутий тип руху. Завдання (аналогічна № 1167 з підручника Атанасян, см. Список літератури) Побудуйте трикутник, який виходить з даного трикутника ABC поворотом навколо точки А на кут 60 ° проти годинникової стрілки (ΔАВС). Рішення (Рис. 3).При повороті точка А перейде в саму себе. Точки В і С перейдуть в точки В1 і С1 відповідно. Кути трикутника і довжини його сторін, відповідно до загальних властивостями руху, збережуться (всі позначення сторін і кутів дані на Рис. 3). Побудови при повороті вкрай за до циркуля побудувати дугу кола радіусом, рівним довжині сторони трикутника (АС або АВ), з центром в точці А, далі за до транспортира відкласти на дузі кут 60 ° і відзначити точку-образ (В1 або С1) . Поєднавши отримані точки-образи відрізками, можна отримати шуканий трикутник А1У1С1, що є чином трикутника АВС (ΔАВС = ΔА1В1С1). Точка О є точкою перетину биссектрис рівностороннього трикутника ABC. Доведіть, що при повороті навколо точки О на кут 120 ° трикутник ABC відображається на себе. Рішення.Точка О перетину биссектрис правильного трикутника є центром цього трикутника. Отже, вершини трикутника при повороті навколо точки О будуть «малювати» дуги кола, описаного навколо ΔАВС. Легко показати, що ÐВОС = ÐСОА = ÐАОВ = 120 °. Отже, при повороті, точка А перейде в точку В, точка В перейде в точку С і точка С перейде в точку А (нагадаємо, що кут повороту вважається позитивним, якщо поворот відбувається проти годинникової стрілки). Таким чином, ΔАВС = ΔАВС. Завдання вирішена. Завдання. Дана пряма, на якій задані точка О1 і точка О2 і дано точки А і В, що лежать по різні боки від цієї прямої. Причому мають місце рівності відстаней: О1А = О1В, О2А = О2В. Довести, що точки А і В симетричні щодо зазначеної прямий. Рішення (Рис. 5).Для доказу необхідного в завданню затвердження нам необхідно довести, що АМ = МВ і АВ ^ О1О2. Побудуємо коло радіусом О1А з центром в точці О1 і коло радіусом О2А з центром в точці О2. Розглянемо деяку осьову симетрію з віссю О1О2. При такому відображенні півкола, розташовані у верхній півплощині, перейдуть до відповідних півкола, розташовані в нижній півплощині щодо осі симетрії. При цьому точка перетину «верхніх» півколо - точка А - перейде в точку перетину «нижніх» півколо - точку В. Тобто точка В симетрична точці А відносно даної прямої. Завдання вирішена. На закінчення розберемо ще один застосування понять симетрії. Дан паралелограм ABCD. Довести, що точка перетину його діагоналей є його центром симетрії. Нагадування: фігура називається симетричною відносно точки О, якщо для кожної точки фігури симетрична їй точка щодо точки Про також належить цій фігурі. Точка О називається центром симетрії фігури. Кажуть також, що фігура має центральну симетрію.

4,8(88 оценок)

Ответ:

alisavakhnina1

14.02.2023

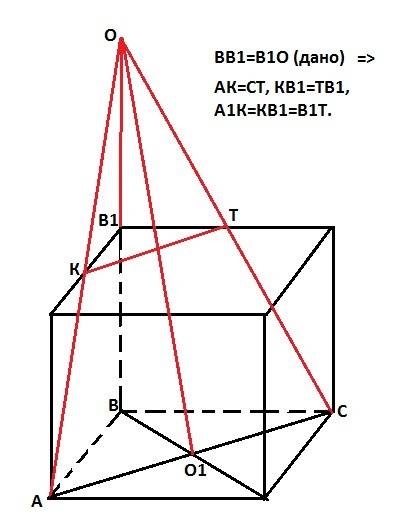
1. АВСD - квадрат. Диагонали квадрата взаимно перпендикулярны и точкой пересечения О1 делятся пополам. Следовательно, прямая ОО1 - перпендикулярна АС по теореме о трех перпендикулярах, так как ВО (перпендикулярная АС) - проекция наклонной ОО1. Тогда треугольник АОС - равнобедренный (ОО1 - высота, медиана и биссектриса), АО=ОС и КТ - его средняя линия (так как ВВ1=В1О - дано) => АК=ТС => четырехугольник АКТС - равнобедренная трапеция. Что и требовалось доказать.

2. Средняя линия трапеции - полусумма ее оснований. АС=2√2см (диагональ квадрата со стороной = 2см), а КТ=√2 (по Пифагору, так как треугольник КВ1Т - прямоугольный, равнобедренный, с катетами = 1). Тогда средняя линия трапеции равна 1,5*√2 см.