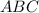 , в который вписана окружность
, в который вписана окружность 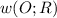
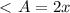
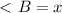
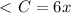
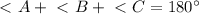
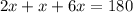
 -
- 
 -
- 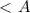
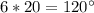 -
- 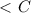
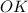 ⊥
⊥ 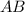
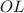 ⊥
⊥ 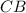
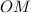 ⊥
⊥ 
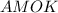
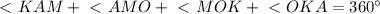
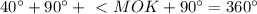
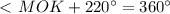
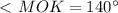
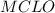
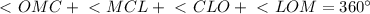
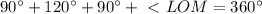
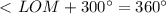
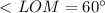
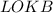
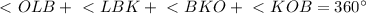
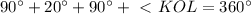
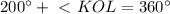
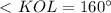
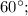
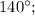
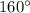
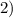
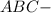 равнобедренный, значит
равнобедренный, значит 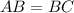
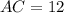 см
см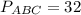 см
см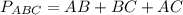 , так как
, так как 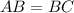 , то
, то 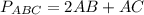
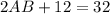
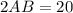
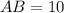 (см)
(см) 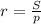 , где
, где 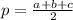 или
или 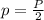
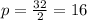
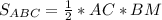
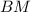 ⊥
⊥ 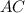 и
и 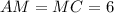
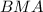 - прямоугольный
- прямоугольный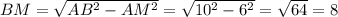 (см)
(см)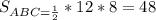 (см²)
(см²)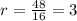 (см)
(см)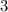 см
см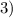
 равнобедренная трапеция, около которой описана окружность
равнобедренная трапеция, около которой описана окружность 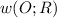
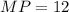 см
см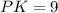 см
см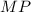 ⊥
⊥ 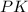 ( по условию)
( по условию)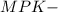 прямоугольный
прямоугольный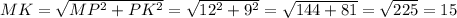 см
см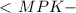 вписанный угол и
вписанный угол и 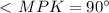 , значит опирается на диаметр окружности
, значит опирается на диаметр окружности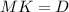
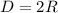
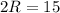
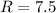
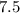 см
см


Найти: высоту SO.
Построение. К основанию треугольника АВС проведем высоту ВН, которая будет являться и медианой и биссектрисой, так как треугольник равнобедренный. Отрезок SH также является высотой, так как треугольник ASC равнобедренный. Значит, угол SHB - заданный в условии двугранный угол. Высота пирамиды проецируется на основание в точку О, являющуюся центром вписанной в треугольник АВС окружности, так как все грани пирамиды наклонены к основанию под одинаковым углом.
Решение: Рассмотрим прямоугольный треугольник OSH:
Неизвестным остается отрезок НО, являющийся радиусом ранее упомянутой окружности.
Площадь треугольника равна половине произведения его основания на высоту, проведенную к основанию. С другой стороны площадь треугольника равна произведению его полупериметра на радиус вписанной окружности. Приравнивая эти площади, получим:
BH найдем из треугольника АВН по теореме Пифагора, учитывая, что АН - половина АС.
ответ: