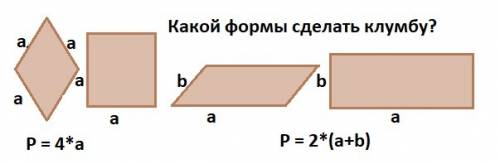
В задаче не сказано какой формы будут клумбы - вот и задумался садовник. Рисунок к задаче в приложении.
Если стороны равны - а , то это ромб или квадрат. Тогда периметр по формуле: Р = 4*а.
Если стороны разные: a и b, то это параллелограмм или прямоугольник и периметр по формуле: P = 2*(a + b).
1) а = b = 4 м. Р1 = 4*а = 4*4 = 16 м - периметр первой клумбы.
2) Р2 = 2*(6 + 4) = 2*10 = 20 м - периметр второй клумбы
3) Р3 = 2*(7 + 2) = 2*9 = 18 м - периметр третьей клумбы.
4) Р4 = 2*(5 + 3) = 2*8 = 16 м - периметр четвёртой клумбы.
И теперь длину изгороди на все четыре клумбы - сумма отдельных.
5) Р = 16+20+18+16 = 70 м на все четыре клумбы - ОТВЕТ
В решении.
Пошаговое объяснение:
При каких наибольшем и наименьшем натуральных значениях х выполняется неравенство 7 < 70-9х < 43?
Можно решать двойное неравенство через систему неравенств, но есть более наглядный
1) Из всех частей неравенства вычесть 70:
7 - 70 < 70 - 70 - 9x < 43 - 70
Неравенство примет вид:
-63 < -9x < -27
2) Разделить все части неравенства на -9 (знак неравенства при этом изменится на противоположный):
7 > x > 3
Решение неравенства: х∈(3; 7).
Неравенство строгое, х=3 и х=7 не входят в решения неравенства, значит, наименьшим натуральным решением будет х=4, а наибольшим х=6.