№1:  . №2:
. №2: 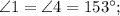
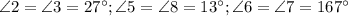 .
.
№1.
Пусть  , тогда
, тогда  - секущая.
- секущая.
Теорема: "При пересечении двух параллельных прямых секущей, сумма односторонних углов равна  .
.
 , по условию.
, по условию.
 и
и  - односторонние углы
- односторонние углы 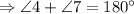
№2.
Обозначим данные прямые буквами 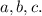
Пусть  - секущая прямых
- секущая прямых  и
и 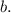
Теорема: "При пересечении двух параллельных прямых секущей, накрест лежащие углы равны".
 и
и 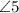 - накрест лежащие при пересечении
- накрест лежащие при пересечении  и
и  секущей
секущей  , однако
, однако 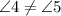 .
.

 и
и  - не параллельны.
- не параллельны.
============================================================
Свойство: "Вертикальные углы равны".
Свойство: "Сумма смежных углов равна  ".
".
Рассмотрим углы, образовавшиеся при пересечении прямых  и
и 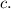
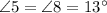 , по свойству вертикальных углов.
, по свойству вертикальных углов.
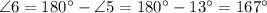 , по свойству смежных углов.
, по свойству смежных углов.
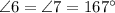 , по свойству вертикальных углов.
, по свойству вертикальных углов.
===========================================================
Рассмотрим углы, образовавшиеся при пересечении прямых  и
и  .
.
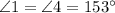 , по свойству вертикальных углов.
, по свойству вертикальных углов.
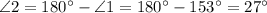 , по свойству смежных углов.
, по свойству смежных углов.
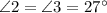 , по свойству вертикальных углов.
, по свойству вертикальных углов.
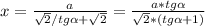
1) Пусть точка M лежит вне окружности. O - центр окружности, точка T - пересечение отрезка OM и окружности. Возьмем на окружности точку T1, не лежащую на OM. В треугольнике MT1O сторона OM меньше суммы двух других сторон (неравенство треугольника),
MT+OT<MT1+OT1 <=> MT<MT1 (OT=OT1, радиусы)
Таким образом, чтобы длина MT была минимальной, T должна лежать на OM. Если M вне окружности, MT=1, OT=2000, то OM=MT+OT=2001. Искомое ГМТ - окружность радиусом 2001 с центром данной окружности.
2) Аналогично доказывается, что если точка M лежит внутри окружности, то искомое ГМТ - окружность радиусом 1999 (OM=OT-MT) с центром данной окружности.