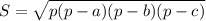, здесь a,b,c - стороны треугольника, p - полупериметр треугольника (в нашем случае a=4, b=13, c=15, 
).
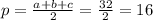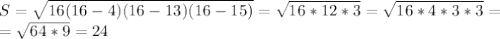
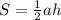, где a - сторона треугольника, h - проведённая к ней высота. Обозначим за h₁ высоту, проведённую к стороне a, за h₂ высоту, проведённую к стороне b и за h₃ высоту, проведённую к стороне c. Тогда 2S=ah₁=bh₂=ch₃. Так как в нашем случае a<b<c, то h₁>h₂>h₃. Значит, наибольшая высота - та, которая проведена к стороне, равной 4. Если сторона равна 4, а площадь равна 24, то из формулы площади треугольника легко найти высоту:
Пусть угол при основании b, длина основания L, радиусы r и R;
2*b = 180 - a; b = 90 - a/2; b/2 = 45 - a/4;
L = 2*R*sin(a); теорема синусов.
r /(L/2) = tg(b/2); центр вписаной окужности лежит на биссектрисе.
r = R*sin(a)*tg(b/2);
r/R = sin(a)tg(45 - a/4); ну, вообще то это уже ответ :))) упростим. Я из чувства лени :)) просмотрел вагон сайтов с формулами, но почему то связь между тангенсом угла и функциями двойного угла не нашел, хотя всегда считал это табличными формулами.. Странно, но получаются они элементарно. Умножаем и делим на 2*соs(45 - a/4);
r/R = sin(a)*(2*sin(45 - a/4)*cos(45 - a/4))/((2*(cos(45 - a/4))^2) - 1 + 1);
r/R = sin(a)*sin(90-a/2)/(cos(90 - a/2)+1) = sin(a)*cos(a/2)/(sin(a/2)+1);
Дальше упрощать смысла нет.
для равностороннего треугольника r/R = 1/2, формула дает ту же величину.