Поиск...
3
Избавься от ограничений
ПОПРОБУЙ ЗНАНИЯ ПЛЮС СЕГОДНЯ
Ruvioo
26.01.2015
Геометрия
5 - 9 классы
ответ дан • проверенный экспертом
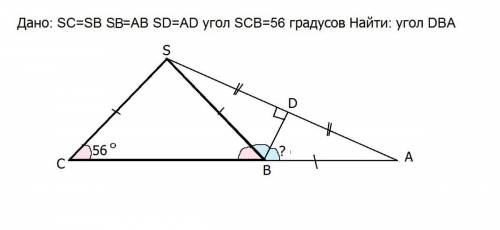
! Дано: SC=SB Sb=AB SD=AD угол SCB=56 градусов Найти: угол DBA
1
СМОТРЕТЬ ОТВЕТ
ответ, проверенный экспертом
3,0/5
19
Hrisula
главный мозг
7.7 тыс. ответов
83.3 млн пользователей, получивших
Треугольник SCB - равнобедренный по условию.
Углы при основании СВ равны. Угол SBC =SCB=56°
Угол SBA cмежный и равен 180°- 56°=124°
В треугольнике SBA по условию SB=BA, он тоже равнобедренный.
SD=DA, следовательно, ВD - медиана.
В равнобедренном треугольнике медиана является биссектрисой и высотой.
ВD - биссектриса,⇒ угол АBD - половина угла SBA и равен 124°:2=62°
Можно найти и угол DSB
Треугольник SDB- прямоугольный, т.к. ВD - высота.
Угол DSB равен 90°-62°=28°
В правильном тетраэдре все грани - равные равносторонние треугольники.
Площадь одной грани:
S₁ = a²√3/4 = 4²√3/4 = 4√3 см²
Так как К - середина DC, то АК = ВК - медианы и высоты равных треугольников DAC и DBC. Тогда
Sakd = Sbkd = 1/2 S₁ = 2√3 см² - это площади двух боковых граней пирамиды KABD.
Пусть Н - середина АВ, так как треугольник АКВ равнобедренный, то КН - его высота.
СН = DH = а√3/2 = 4√3/2 = 2√3 см как медианы и высоты равных равносторонних треугольников.
Тогда ΔDHC равнобедренный, КН - его медиана и высота:
КН⊥CD.
ΔСКН: ∠СКН = 90°, СН = 2√3 см, СК = CD/2 = 2 см, по теореме Пифагора
КН = √(CH² - CK²) = √((2√3)² - 2²) = √(12 - 4) = √8 = 2√2 см
Sabk = 1/2 AB · KH = 1/2 · 4 · 2√2 = 4√2 см²
Площадь боковой поверхности пирамиды KABD:
Sбок = Sakd + Sbkd + Sabk = 2√3 + 2√3 + 4√2 = 4(√3 + √2) см²
360:45=8 м
вот так