S1 = S2 = 2/3 ед². S3 = 1/3 ед². S4 = 4/3 ед² = 1 1/3ед².
Объяснение:
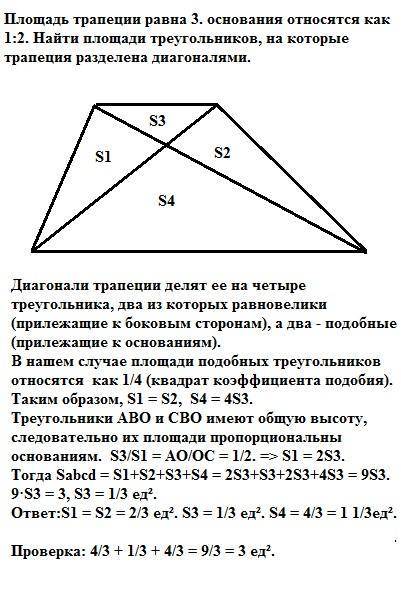
Диагонали трапеции делят ее на четыре треугольника, два из которых равновелики (прилежащие к боковым сторонам), а два - подобные (прилежащие к основаниям).
В нашем случае площади подобных треугольников относятся как 1/4 (квадрат коэффициента подобия). Таким образом, S1 = S2, S4 = 4S3.
Треугольники АВО и СВО имеют общую высоту, следовательно их площади пропорциональны основаниям. S3/S1 = AO/OC = 1/2. =>
S1 = 2S3.
Тогда Sabcd = S1+S2+S3+S4 = 2S3+S3+2S3+4S3 = 9S3.
9·S3 = 3, S3 = 1/3 ед².
ответ:S1 = S2 = 2/3 ед². S3 = 1/3 ед². S4 = 4/3 = 1 1/3ед².
Проверка: 4/3 + 1/3 + 4/3 = 9/3 = 3 ед².
построй точки Х Х' Y
соедини точки Х Х' -отрезком--найди середину--это центр симметрии О
проведи от Y через О отрезок Y Y' точка Y' -симметричная Y