У прямой y = -8x + 9 находим точку, которая принадлежит оси ординат.
При этом х = 0, тогда у = 9. Точка А(0; 9).
Для параллельной прямой угловой коэффициент сохраняется.
у = 4х + в. Подставим координаты точки А, через которую должна пройти прямая.
9 = 4*0 + в, отсюда в = 9.
ответ: у = 4х + 9.
Это общее решение такого рода задания, Для данной задачи можно было решить проще, так ка слагаемое "в" в уравнении прямой равно координате "у" в точке пересечения прямой оси Оу. У нас это 9.
С учётом равенства угловых коэффициентов сразу получаем уравнение параллельной прямой у = 4х + 9.
РЕШЕНИЕ:
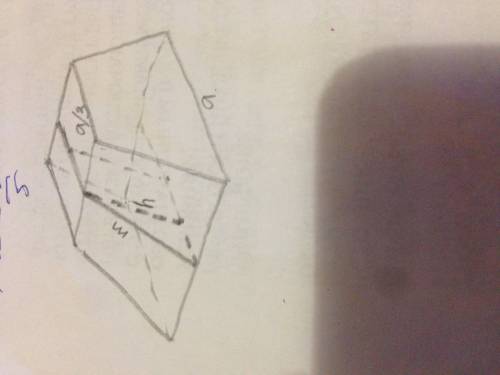
• SABCD - правильная четырёхугольная пирамида, так как все его рёбра равны. В основании этой пирамиды лежит квадрат со стороной, равной АВ = Р abcd / 4 = 16 / 4 = 4 см.
• MNPTOFCK - наклонная призма, все рёбра которого равны по 2 см. Стороны верхнего основания являются средними линиями боковых граней, стороны нижнего основания равны половине сторон квадрата ABCD. Соответственно, в призме
MNPTOFCK в основаниях лежат квадраты, а боковые грани - ромбы.
• Для того чтобы найти объём призмы, необходимо знать площадь основания и высоту призмы.
• Верхнее основание призмы делит высоту SO данной пирамиды на две равные части, так как в тр. АСS МР - средняя линия. К тому же тр. АСS - равнобедренный, прямоугольный, по тому следствию, что тр. АВС = тр. АСS по трём сторонам. В правильной четырёхугольной пирамиде высота проецирется в центр основания, поэтому АО = ОС = DO = OB. В прямоугольном треугольнике медиана, проведённая в гипотенузе, равна её половине, то есть АО = ОС = SO.
• В тр. АВС: по т. Пифагора АС = V( 4^2 + 4^2 ) = 4V2 см ; AO = OC = AC/2 = 4V2 / 2 = 2V2 см ; SН = НO = SO/2 = AO/2 = 2V2 / 2 = V2 см.
• V призмы = S ofck • HO = 2 • 2 • V2 = 4V2 см^3
Также можно заметить, что V sabcd = S abcd • SO / 3 => 3•V sabcd = S abcd • SO
V призмы = S ofck • HO = ( S abcd/4 ) • ( SO/2 ) = S abcd • SO / 8 = 3•V sabcd / 8
ОТВЕТ: 4V2 см^3.