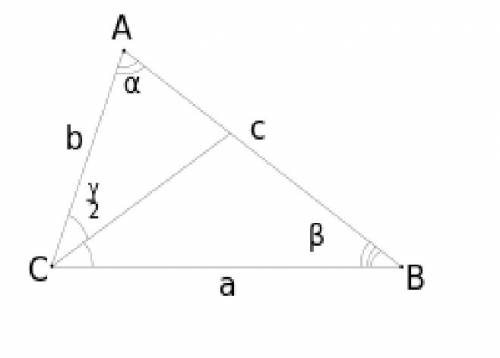
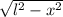Луч oe делит угол aob на два угла.
найдите ∠eob, если ∠aoe=27 градусов; ∠aob=57 градусов

👇

Увидеть ответ

Ответ:

не0тличник

31.05.2020

∠ЕОВ=∠АОВ-∠АОЕ=57-27=30°

Объяснение:

4,5(69 оценок)

Открыть все ответы

Ответ:

VladimirLK

31.05.2020

Развёртка есть :) Это самое простое.
на рис.2 - диагональное сечение пирамиды, через диагональ основания и вершину
Диагональ основания по Пифагору
d² = a² + a²
d = a√2
стороны длиной а см
Видно, что это прямоугольный треугольник, точно такой же, как половинка основания
Его площадь через катеты
S = 1/2*a*a
Его площадь через гипотенузу и высоту к ней
S = 1/2*d*h
a*a = d*h
a² = a√2*h
h = a/√2 - это высота пирамиды
рис 3.
Боковая грань пирамиды представляет собой равносторонний треугольник - ведь все рёбра равны а
Для нахождения апофемы возьмём половину этого треугольника
По т. Пифагора
a² = (a/2)² + f²
f² = 3/4*a²
f = a√3/2
---
Площадь - это основание и 4 боковушки
S = a² + 4*1/2*a*f = a² + 2*a*a√3/2 = a²(1 + √3)
Объём
V = 1/3*a²*h = 1/3*a²*a/√2 = a³/(3√2)

Найдите апофему, высоту, площадь полной поверхности и объем правильной четырехугольной пирамиды, у к

Найдите апофему, высоту, площадь полной поверхности и объем правильной четырехугольной пирамиды, у к

4,4(77 оценок)

Ответ:

heyguys112

31.05.2020

1) Во-первых, треугольник в котором две биссектрисы равны является равнобедренным. Отсюда сразу напишем ответ: p=9+9+6 = 24 см;
Теперь докажем утверждение 1)
Возьмем угол и проведем в нем биссектрису данной длины. Пусть длина равна l. Теперь будем выбирать точки на луче (назовем его луч 1) данного угла и через конец биссектрисы проводить множество прямых. Они будут пересекаться со вторым лучом угла и будут образовывать угол с ним. Рассмотрим множество получившихся углов. Из каждой вершины угла проведем ее биссектрису до пересечения с лучом 1. Исключим из рассмотрения все биссектрисы длины которых не равны l; Итак, перед нами множество биссектрис с длинами l; Докажем, что любые две могут образовать треугольник. Рассмотрим две крайние биссектрисы. Расстояние между ними $\sqrt{l^{2}-x^{2}}$ , где x - расстояние AB (см. рис.); Это первая сторона треугольника. Две другие равны l; Очевидно, что 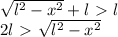$\sqrt{l^{2}-x^{2}}+l\ \textgreater \ l \\ 2l\ \textgreater \ \sqrt{l^{2}-x^{2}}$ ; Поэтому с любые две биссектрисы образуют треугольник. С другой стороны, в равнобедренном тупоугольном треугольнике не могут быть равны основание и сторона. Значит множество рассматриваемых биссектрис может содержать лишь одну биссектрису длины l; Другими словами, существует лишь один треугольник с двумя равными биссектрисами данной длины и с данным единственным углом. Но для таких параметров легко подобрать равнобедренный треугольник, в котором очевидно равны биссектрисы, выходящие из равных углов. Значит найденный нами единственный треугольник - равнобедренный, что и доказывает утверждение (1);
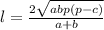Доказать можно было проще: формула биссектрисы - $l= \frac{2 \sqrt{abp(p-c)} }{a+b}$ ; Другой биссектрисы: 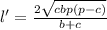$l'= \frac{ 2\sqrt{cbp(p-c)} }{b+c}$ ; Поскольку l=l', то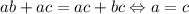 $ab+ac=ac+bc \Leftrightarrow a=c$
Дан треугольник abc. am и bk - биссектрисы, am=bk, ab=6 см, bc=9 см. найдите периметр треугольника a