Найти угол x. точка о-центр окружности.
screenshot_5.jpg
2.
из точки а, которая лежит вне окружности с центром в точке о, проведены касательные ав и ас к этой окружности (в и с – точки касания). доказать, что четырехугольник авос можно вписать в окружность.
3.
в параллелограмме abcd ae – биссектриса угла а. стороны параллелограмма ав и вс относятся как 4: 9. ае пересекает диагональ bd в точке к. найти отношение bk: kd.
screenshot_6.jpg
4.
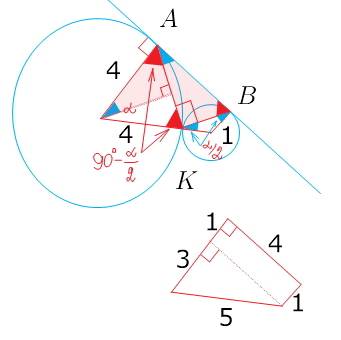
точка касания вписанной окружности делит боковую сторону равнобедренного треугольника на отрезки 3 см и 5 см, начиная от основания. найдите периметр треугольника.
РА=10 см, РО=8 см, <POA=90°
ΔPOA. по теореме Пифагора: AO²=PA²-PO²
AO²=10²-8², AO²=36, AO =6 см.
ΔADC: AC=2AO, AC=12 см, AD=DC=a
по теореме Пифагора: AO²=AD²+CD²
12²=a²+a², 144=2a², a²=72, a=√72, a=6√2 см
ответ: сторона основания АВ=6√2 см
2. Sбок.пов. =(1/2)Pосн*h
h - апофему боковой грани правильной пирамиды найдем по теореме Пифагора из ΔАКР: PK_|_AB, AK=(1/2)AB, AK=3√2 см
PA²=AK²+PK², 10²=(3√2)²+PK², PK²=100-18, PK²=82, PK=√82 см
S=(1/2)*4*6√2*√82=12√164=12√(4*41)=24√41
S бок.=24√41 см²