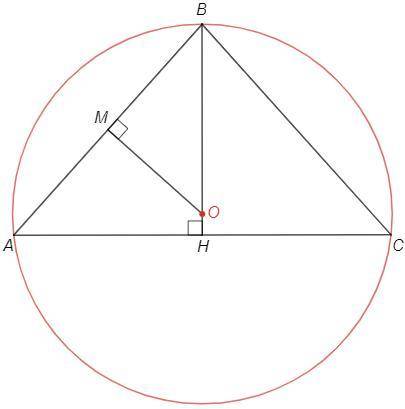
В равнобедренном треугольнике высота к основанию является также биссектрисой и медианой.
BH - высота/биссектриса/медиана
AC=4x, AB=3x
AH =AC/2 =2x
BH =√(AB^2 -AH^2) =√(9-4) x =√5 x (т Пифагора)
Центр вписанной окружности - пересечение биссектрис.
AI - биссектриса
По теореме о биссектрисе
BI/IH =AB/AH =3/2 => IH =2/5 BH =8 (см)
Центр описанной окружности - пересечение серединных перпендикуляров.
MO - серединный перпендикуляр к AB
AB/BH =3/√5 => AB =3/√5 BH =12√5
△OBM~△ABH (прямоугольные с общим углом)
OB/AB =BM/BH => OB/12√5 =6√5/20 => OB =18 (см)
Или
cosA =2/3
sinC =sinA =√(1 -cosA^2) =√5/3
AB =BH/sinA
AB/sinC =2R (т синусов) => R =BH/2sinA^2 =20/2 :(5/9) =18 (см)

А(100, -14)
3*100+13= (-14)
313=(-14)
Не належить
В(-18,41)
3*(-18)+13=41
-54+18 = 41
-41=41
Належить
Объяснение:
А(100, -14), В(-18,41)
Проверим точку А
Первая цифра, (100 в нашем случае) отвечает за х, а вторая (в нашем случае (-14)) за у.
Подставляем:
(для удобства переносим у назад, чтобы вышло понятное уравнение)
3*100+13= (-14)
313=(-14) - 313 не = (-14), поэтому, точка "А" не принадлежит графику.
Проверим точку В
Первая цифра, ((-18) в нашем случае) отвечает за х, а вторая (в нашем случае 41) за у.
Подставляем:
3*(-18)+13=41
-54+18 = 41
-41=41 - точка "В" принадлежит, так как противоположная
Вообще, площадь ромба можно найти несколькими но нас в данной задаче интересует такой:
S = a²×sinα, где а - сторона ромба, α - известный острый угол. Нам известно, что диагональ делит ромб на два равных между собой ΔΔ, причем один из углов этого Δ равен 30°, значит весь угол равен 2×30 = 60°. Площадь ромба равна (18)²×sin60°. Подставляешь значение sin60°, перемножаешь на (18)² и получаешь искомую цифру.