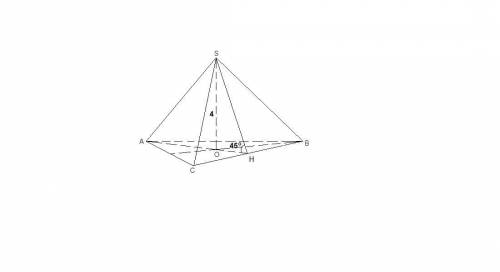
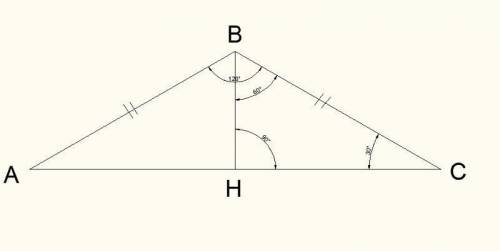
Пусть Н - середина стороны ВС.
АН⊥ВС как медиана и высота правильного треугольника АВС,
SH⊥ВС как медиана и высота равнобедренного треугольника SBC.
∠SHA = 45° - линейный угол двугранного угла между плоскостью боковой грани и плоскостью основания.
ΔSOH: ∠SOH = 90°, ∠SHO = 45°, значит это равнобедренный прямоугольный треугольник, тогда
ОН = SH = 4 м, SH = 4√2 м
ОН - радиус окружности, вписанной в правильный треугольник:
ОН = АВ√3/2
АВ = 2 · ОН / √3 = 2 · 4 / √3 = 8√3/3 м
Sбок = 1/2 Pосн · SH
Sбок = 1/2 · 3 · 8√3/3 · 4√2 = 16√6 м²
∠МON
P-биссектриса ∠МON
Биссектриса - это луч, исходящий из вершины угла и делящий его на два равных угла.
Т.к. Биссектриса исходит из вершины О ∠МON, значит делит его на 2 равных угла: ∠MOP и ∠PON
То есть ∠MOP =∠PON
И, кстати, углы правильнее всего подписывать тремя большими буквами,а точка вершины угла ПОСЕРЕДИНЕ.