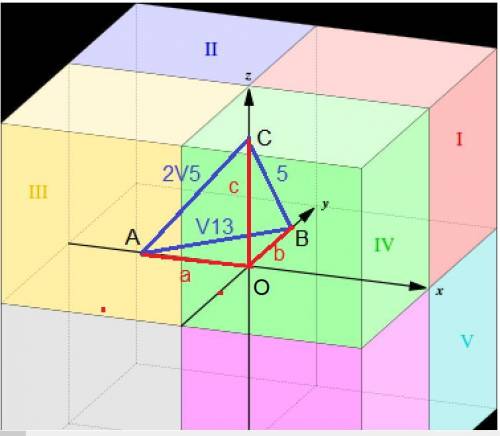
Находим длины отрезков, отсекаемых четвёртой гранью на осях.
Из прямоугольных треугольников с катетами на осях составляем систему.
{a² + c² = (2√5)² {a² + c² = 20
{b² + c² = 5² {b² + c² = 25
{a² + b² = (√13)² {a² + b² = 13.
Из второго уравнения вычтем первое: b² - a² = 5 или b² = a² + 5. Подставим величину b² в третье уравнение:
a² + a² + 5 =13, получаем 2a² = 8, отсюда a² = 8/2 = 4, и а = √4 = -2.
Знак минус по условию расположения точки А.
Величина b = √(a² + 5) = √(4 + 5) = √9 = 3.
Значение с находим из второго уравнения:
C = √(25 - b²) = √(25 - 9) = √16 = 4.
Получаем уравнение плоскости в отрезках.
(x/ (-2)) + (y/3) + (z /4) = 1.
Приведём к общему знаменателю.
(-6x/ 12) + (4y/12) + (3z /12) = 12/12.
Отсюда получаем общее уравнение плоскости.
-6x + 4y + 3z – 12 = 0.
площадь полной поверхности состоит из двух площадей оснований и боковой поверхности. В основании ромб, его площадь ищется по формуле сторона в квадрате умножить на синус угла между сторонами. Т.е. (2√3)²*√3/2= 6√3, но оснований два, поэтому эту площадь умножаем на два. получаем 12√3/см²/
Диагональ ромба по теореме косинусов равна √2(2√3)²-2*(2√3)²1/2=(2√3), а высота призмы находится как диагональ ромба умноженная на tg30°, т.е. (2√3)*(1/√3)=2.
Чтобы найти боковую поверхность, надо периметр основания, т.е. 8√3 умножить на высоту призмы, т.е. на 2 получим 16√3
Сложив теперь полученные площади оснований с площадью боковой поверхности, получим площадь полной поверхности. 12√3+16√3=28√3
ответ верный ответ под номером № 3) , т.е. 28√3
Удачи!