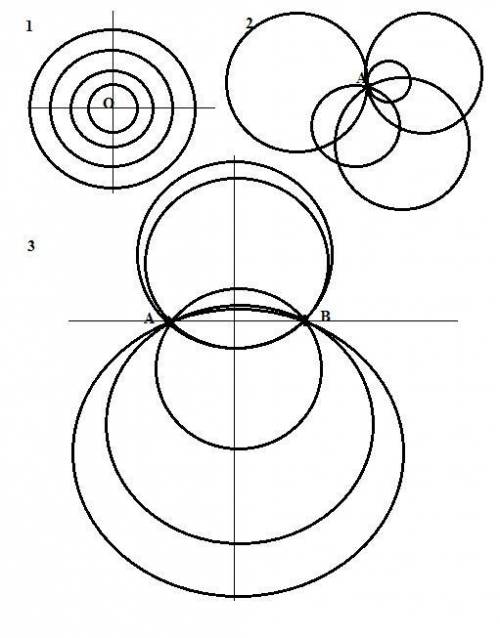
1 - д. 2 - д 3 - д.
Объяснение:
1. Точка может быть центром бесконечного числа концентьрических окружностей (окружностей разных радиусов).
2. Через одну точку можно провести бесконечное число пересекающихся (или касающихся) окружностей.
3. Так как через три точки можно провести единственную окружность, а даны только 2 точки, то третья точка может располагаться в любом месте. Значит через две точки можно провести бесконечное число пересекающихся (имеющих две общие точки) окружностей. Центры этих окружностей будут лежать на серединном перпендикуляре к отрезку АВ.
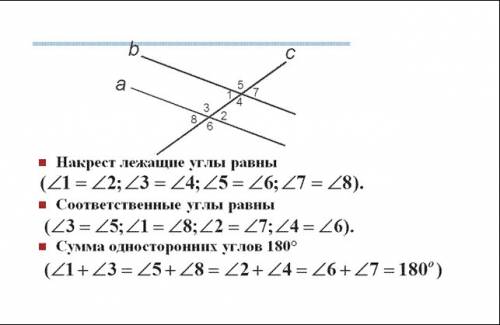
Дано:
a║b
c - секущая
<5 = 113°
Найти <1;<2;<3; <4; <6; <7; <8.
1) <5 = <4 = 113° как вертикальные.
2) <1 и <5 - смежные.
Сумма смежных углов равна 180°.
Отсюда получаем:
<1 = 180°-113° = 67°.
3) <1 = <7 = 67° как вертикальные.
4) <1 = <2 = 67° как внутренние накрест лежащие.
5) <3 = <5 = 113° как соответственные.
6) <1 = <8 = 67° как соответственные
7) <6 = <5 = 113° как внешние накрест лежащие.
ответ: <1 = <2 = <7 = <8 = 67° ;
<3 = <4 = <5 = <6 = 113°
через 2 прямые МР и НО модно провести плоскость, препендикулярную заданной. В этой плоскости МНРО - трапеция, с основаниями НО = 12, МР = 24, и боковой стороной, перпендикулярной основаниям (это в условии задано, что МР и НО препендикулярны плоскости, а РО как раз лежит в этой плоскости, потому что точки Р и О лежат в ней :. Эта боковая сторона РО = 5. Надо найти вторую, так сказать, наклонную боковую сторону трапеции. Как это делается, ясно из следующего соотношения
МН^2 = (МР - НО)^2 + РО^2;
МН^2 = (24 - 12)^2 + 5^2;
МН =13