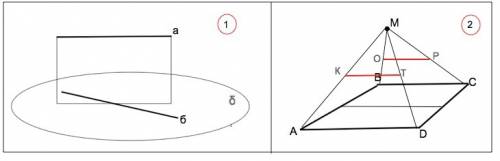
Прямая параллельна плоскости, если не имеет с ней общих точек. Прямая а не может пересекаться с прямой б, т.к. в противном случае будет пересекать и плоскость δ.
Прямые а и б могут быть параллельны или быть скрещивающимися.
====
а)Средняя линия ОР треугольника ВМС параллельна ВС ( по определению). ВС параллельна АD по условию. Если одна из двух параллельных прямых параллельна третьей, то они параллельны. ⇒
ОР║ АD
Средняя линия КТ треугольника АМD параллельна AD ⇒ КТ ║ ОР. Доказано.
б) Средняя линия трапеции равна полусумме оснований.⇒
АD+ВС=2•16=32 см
Примем коэффициент отношения оснований трапеции равным х.
Тогда 5х+3х=32 ⇒
8х=32 см
х=4 см
АD=20 ⇒ KT=20:2=10 см
BC=12 ⇒ OP=12:2=6 см
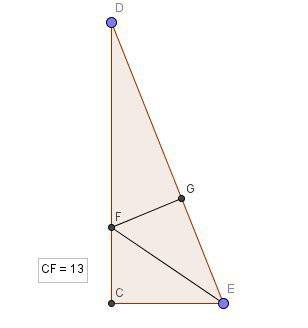
 с прямым углом
с прямым углом  , EF — биссектриса
, EF — биссектриса  ,
,  , FG — искомый отрезок.
, FG — искомый отрезок.  .
.  — биссектриса, то
— биссектриса, то  (биссектриса
(биссектриса  делит
делит  на два равные угла).
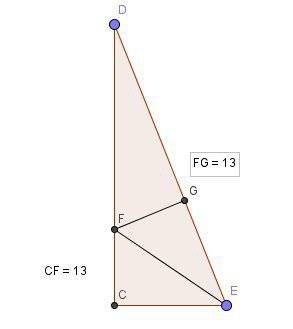
на два равные угла). 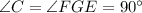 (это следует из условия: так как
(это следует из условия: так как  прямоугольный, то и
прямоугольный, то и  ; так как
; так как  — расстояние от
— расстояние от  до
до 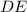 , то
, то 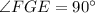 ).
).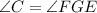 и
и 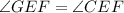 , то и третий угол первого треугольника равен третьему углу второго треугольника:
, то и третий угол первого треугольника равен третьему углу второго треугольника:  . Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так:
. Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так: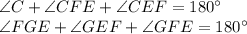
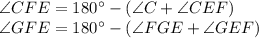
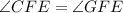 .
.  является для обоих треугольников общей.
является для обоих треугольников общей. (второй признак равенства треугольников — по стороне и двум прилежащим к ней углам (
(второй признак равенства треугольников — по стороне и двум прилежащим к ней углам ( — сторона, а
— сторона, а  — два прилежащих угла)).
— два прилежащих угла)). соответствует
соответствует  , тогда:
, тогда: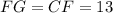
 . Смотрите второй рисунок.
. Смотрите второй рисунок.