1)Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
2)Перпендикулярность прямых и плоскостей в пространстве С понятием перпендикулярности прямой и плоскости мы встречаемся ежедневно. Например, мачты освещения устанавливаются перпендикулярно поверхности земли. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой в этой плоскости.
3)Прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции наклонной на эту плоскость.
4) Угол между прямой и плоскостью - угол между прямой и ее проекцией в данной плоскости
5) две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения плоскостей, пересекает их по перпендикулярным прямым. Признак перпендикулярности плоскостей. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
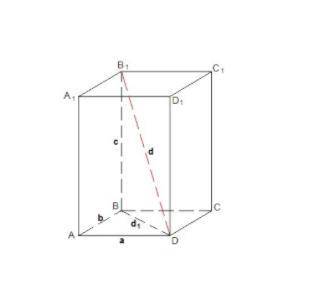
6)Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений:
d² = a² + b² + c²
Доказательство:
Все грани прямоугольного параллелепипеда - прямоугольники.
ΔABD: ∠BAD = 90°, по теореме Пифагора
d₁² = a² + b²
ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора
d² = d₁² + c² = a² + b² + c²
d² = a² + b² + c²
Доказанная теорема - пространственная теорема Пифагора.
Объяснение:
Пикча к последнему
1) тк. треугольник прямоугольный, следовательно один его угол = 90°(прямой), и если бы остальные его углы были равны, то они были бы = 45°( сумма углов треуг. =180°)
2) дано: один из острых углов на 20° больше другого, следовательно можно составить уравнение :
x(первый острый угол) + x+20 (второй острый угол) = 90 ( тк прямой угол = 90, то сумма оставшихся острых = 90)
Решаем : x + x + 20 = 90
2x=90 - 20
2x=70
x = 70: 2
x = 35 ( 1-й острый угол) следовательно второй = 35+20= 55
Но тк в задаче указано найти меньший угол, то ответ будет : 35
AD=10+8=18
KK1=(18+8):2=13
PECD=27
(27-10)÷2=8,5
P=8,5+8,5+18+8=43
ответ будет 43