5) Периметр квадрата со стороной AM равен 4AM.
4AM=2BC <=> AM=BC/2
Отрезок из прямого угла к гипотенузе, равный ее половине - медиана.
AM - медиана и высота, следовательно △ABC - равнобедренный, острые углы 45.
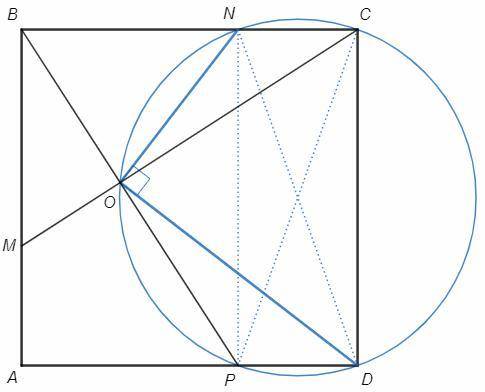
6) Продолжим перпендикуляр BO до пересечения с AD в точке P.
OBM= 90-OMB =BCM
△ABP=△BCM (по катету и острому углу)
AP=BM=BN => PD=NC
PNCD - прямоугольник, диагонали являются диаметрами описанной окружности.
COP=90, точка O лежит на окружности с диаметром CP.
Вписанный угол NOD опирается на диаметр ND, NOD=90
Заданные плоскости на основаниях цилиндра отсекают хорды, являющиеся катетами прямоугольного треугольника.
Эти катеты равны: к1,2 = S1,2/H. Гипотенуза - это диаметр основания.
Тогда осевое сечение равно S = √((S1/H)² + (S2/H)²)*H = √(S1² + S2²) =
= √(45² + 200²) = √(2025 + 40000) = √42025 = 205 кв.ед.