Так как дано, что многоугольник выпуклый, то сумма его внешних углов равна 360 градусам.
Каждый внешний угол равен по 90 градусам, тогда мы сможем узнать количество сторон. Для этого поделим сумму внешних углов на градусную меру каждого угла - 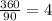
Итак, количество сторон = 4.
Но так как каждый внешний угол прямой, то и внутренние углы этого многоугольника тоже прямые. Тогда получается, что этот многоугольник - прямоугольник (все углы равны между собой).
Но так как у этого многоугольника равны все стороны (по условию) и углы, то это правильный четырёхугольник - квадрат.
ответ: квадрат.
Дано: ΔABE - равнобедренный, АВ=ВЕ= 17 см, АЕ= 16 см, АЕВ∈α, CB⟂α, C∉α, СВ= 8 см.
Найти: расстояние от точки C до стороны треугольника AE
Решение.
1) Проведём высоту ВН в равнобедренном треугольнике АВЕ => BH⟂AE
Так как BH⟂AE и по условию ВС⟂α, по теореме о трёх перпендикулярах следует, что наклонная СН⟂АЕ. Наклонная СН и есть расстоянием от точки С до стороны АЕ ΔABE.
2) В треугольнике ЕСВ (∠ЕВС=90°, т.к. СВ⟂α) по т.Пифагора находим гипотенузу ЕС:
ЕС²= ЕВ²+ВС²;
ЕС²= 17²+8²;
ЕС²= 289+64;
ЕС²= 353
3) Поскольку ΔABE - равнобедренный, а ВН - высота, проведённая к основанию АС, то ВН также является и медианой ΔАВЕ => АН=НЕ= ½АЕ= 16 : 2 = 8 см.
4) В ΔCHE (∠CHE=90°) по т.Пифагора находим СН:
СН²= ЕС² – НЕ²;
СН²= 353–8²;
СН²= 353–64;
СН²= 289;
СН= 17 см (–17 быть не может)
Расстояние от точки C до стороны треугольника AE равно 17 см.
ответ: 17 см.