в условии ошибка, нужно так:
m не делится на n и имеет от деления на n тот же остаток
решение:
a,b - натуральные числа (целые части от деления)
r -остаток от деления
m=na+r
m+n=(m-n)b+r
m+n-r=(m-n)b
n+m-r делится на n и m-nесли m< =2n, тоn< n+m-r< 3n, следовательно оно равно 2nтогда m-n=r и при делении на него не может быть остатка r.значит m> 2nтогда n+m-r< 3(m-n), т.к. 4n< 2mзначит n+m-r=2(m-n), т.к. m-n на n по условию не делится.отсюда m=3n-r, m+n-r=4n-2r делится на n, отсюда r=n/2.значит m=5k, n=2k
m: n=5: 2
Треугольник с прямым углом - это прямоугольный треугольник.
Так как меньшие стороны "прилегают" к прямому углу, то эти стороны - катеты.
Так как катеты имеют длины 6 см и 8 см, то также такой треугольник - египетский (треугольник с соотношением сторон, равным 3:4:5). Следовательно, гипотенуза равна 10 см (можно также проверить через теорему Пифагора).
Высота, проведённая к большей стороне - высота, проведённая к гипотенузе (так как гипотенуза - самая большая сторона в прямоугольном треугольнике).
Высота, проведённая к гипотенузе равна произведению катетов, делённому на гипотенузу.
То есть -
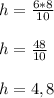
h = 4,8 см.
ответ: 4,8 см.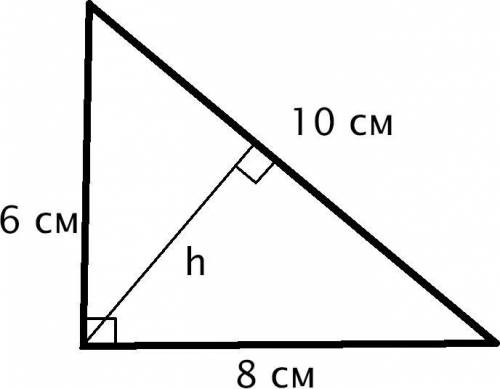
Продлим АВ за точку А, пусть F лежит на этом продолжении и FB = 1.
FBCD - квадрат со стороной 1. Точка пересечения АЕ и FD обозначим за К.
В условии ED + AB = 1, это означает, что FA = ED;
Если провести окружность радиусом 1 и центром в А, то она коснется DC в точке Р, причем АР перпендикулярно DC, FA = PD. Окружность пройдет через точку Е (АЕ =1),
и DE = DP. Поэтому DE - касательная, и треугольник EDK прямоугольный, угол АЕD прямой. Значит треугольники FAK и KED равны, равны и их площади. Поэтому площадь пятиугольника равна площади квадрата, то есть 1.