1. проводим прямму а (базовое построение)
2. обозначем точку А на пряммой а (базовое построение)
3. Через точку А проводим пряммую с, перпендикулярную пряммой а (базовая задача на построение)
4. Откладываем от точки А отрезки АС и АВ длиной равные данному отрезку 1. (базовое построени). Получим прямоугольный треугольник, гипотенуза которого равна ВС=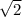
5. Продолжаем отрезок 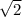от точки С на отрезок равный данному, получим большой отрезок длинной ВР=1+\sqrt{2} (базовое построение)
6. На єтой же пряммой далее от точки Р откладываем отрезок РК равный данному с длиной 1.
7. Делим отрезок ВК пополам (базовая задача на построение)
8. Из середины О отрезка ВК радиусом ВО проводим окружность (базовое построение)
9. Через точку Р проводим перпендикулярную пряммую РХ,(базовая задача на построение) она пересечет окружность в двух точках, берем одну из них обозначаем Н,
отрезок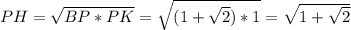 
искомый
Одна сторона прямоугольника равна х, х>0, вторая у, у>0. Площадь прямоугольника S = xy = 2 откуда y = 2/x. Рассмотрим функцию:
P(x)=2х+2у=2х+2*2/х=2х+4/х
Найдем производную этой функции, приравняем к нулю, получим критические точки
2-(4/х²)=0, откуда 4-2х²=0
х²≠0, х=±√2
Поскольку отрицательный корень x = -√2 не подходит по смыслу задачи, то берем критическую точку х=√2, разбиваем ею числовую ось и проверяем, какие знаки принимает производная на интервалах (0;√2);(√2;+∞)
(0)___-(√2)+
Производная функции при переходе через точку x = √2 меняет знак с минуса на плюс, поэтому х=√2 - точка минимума функции.
у=2/√2=√2
А наименьший периметр прямоугольника будет равен 4√2, если обе стороны равны √2, т.е. когда прямоугольник превратится в квадрат.
Диаметр равен двум радиусам, то есть 14,5 умножаем на два. Получаем 29мм.