Формула суммы углов многоугольника
N=180°•(n-2), где n - число сторон многоугольника.
N=180°•3=540°
Все углы правильного многоугольника равны.
Каждый из них равен 540°:5=108°
Все стороны правильных многоугольников равны.
Углы при основаниях равнобедренных ∆ ЕАD и ∆ ВАD равны по (180°-108°):2=36°⇒
∠DAC=108°-36°-36°=36°
∠ЕАD=∠DAC=∠CAB - доказано.
Вариант б)
Около правильного многоугольника можно описать окружность.
Опишем её.
Стороны правильного многоугольника – равные хорды.
Равные хорды стягивают равные дуги.
Вписанные углы, опирающиеся на равные дуги, равны.
∠ЕАD=∠DAC=∠CAB - доказано.
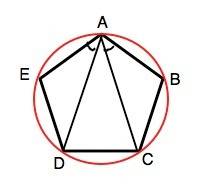
см. приложение
Проведем высоту h1. В равнобедренном треуголника высота, проведенная к основанию, является медианой.
По теореме Пифагора: h1^2=R^2-(0,5a)^2=225
h1=15.
Аналогично сделаем и во втором треугольнике
h2^2=R^2-(0,5b)^2=49
h2=7
Расстояние между хордами равно сумме высот треугольника.
расстояние=h1+h2=15+7=22см