одна из равних стоорн равнобедренного треугольника расчитывается по формуле:
а = b / (2 cosα), где b - основание и равно у нас 6, а α - угол, прилижащий к основанию и равен у нас 30 градусов
Подставляем:
а = 6 / (2 cos (30)) = 6 / (2*√3/2)= 6 / √3 = 6√3 / 3 = 2√3 (см)
А т.к у нас треугольник - равнобедренный, то биссектриса является и медианой, а следовательно lделит основание по полам 6/2 = 3 см
и также является и высотой, а следовательно воспользуемся теормой Пифагора:
a² + b² = c²
где а - катет и он равен у нас 3 (см)
b - втоой катет, котоый надо найти
c - гипотенуза и равна у нас 2√3 см
Подставляем:
3² + b² = (2√3)²
9 + b² = 12
b² = 12-9
b² = 3
b=√3 - длина биссектрисы
ответ: длина биссектрисы равна √3 см
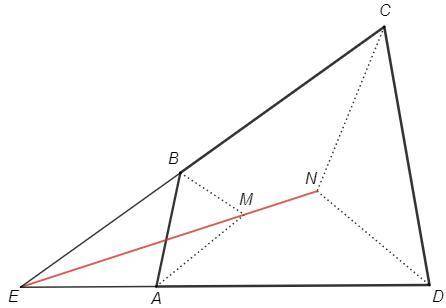
1) AD не параллельна BC, они пересекаются в точке E.
M - точка пересечения биссектрис внешних углов △AEB =>
M лежит на биссектрисе ∠E.
N - точка пересечения биссектрис △CDE =>
N лежит на биссектрисе ∠E.
Если MN перпендикулярна AB, то в △AEB совпадают биссектриса и высота.
Тогда △AEB - равнобедренный, углы при основании равны.
Углы A и B четырехугольника равны как смежные с равными.
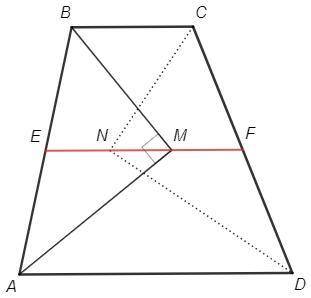
2) AD параллельна BC, трапеция.
Биссектрисы внутренних углов при параллельных пересекаются под прямым углом.
Пусть E - середина AB.
ME - медиана из прямого угла, ME=AB/2
△BEM - равнобедренный, ∠EMB=∠EBM=∠CBM
ME||BC (по накрест лежащим) => M лежит на средней линии трапеции.
Аналогично N.
Если средняя линия перпендикулярна боковой стороне, то трапеция прямоугольная, ∠A=∠B=90.
AB(2-5;-2-(-1);4-3)
AB(-3;-1;1) координаты вектора
Ха,Ya,Za-координаты начала вектора
Xb,Yb,Zb-координаты хвоста вектора
сам вектора это "из конца вычесть начало"