Утриугольника abc бисектриса угла bb1 делит его на два равнобедренных триугольника, при чем ab=bb1=cb1. найти грудусную меру углов триугольника acb

👇

Увидеть ответ

Ответ:

rada201

15.03.2023

Объяснение:

1) Рассмотрим треугольник АВВ1 и треугольник СВВ1

АВ= СВ1(по условию)

ВВ1 - общая

угол АВВ1 = СВВ1(т.к. ВВ1 - биссектриса)

из этого всего следует, что

треугольник АВВ1= треугольнику СВВ1

из этого следует, что эти треугольники равносторонние

из этого следует, что треугольник АВС тоже равносотонний

значит углы равны по 60°

4,5(88 оценок)

Открыть все ответы

Ответ:

Marina1023

15.03.2023

ответ: 7 см, 8 см.

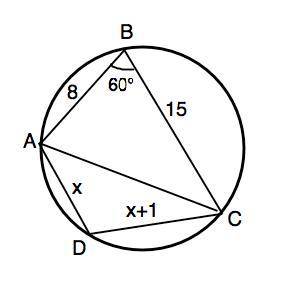
Объяснение: Четырехугольник может быть вписан в окружность только тогда, когда сумма его противоположных углов равна 180°.⇒ Если угол АВС=60°, то угол АDC=120°.

Пусть АВ=8 см, ВС=15 см.

По т.косинусов из ∆ АВС диагональ АВСD АС²=AB²+BC²-2•AB•BC•cos60°

АС²=8²+15²-2•8•15•0,5⇒

AC²=169

В ∆ АDC примем АD=x, DC=х+1.

cos120°=-cos60°=(-0,5)

По т.косинусов АС²=x²+(x+1)²-2•x•(x+1)•(-o,5), откуда

169=3x²+3x+1 ⇒

3x²+3x-168=0

Решив квадратное уравнение, получим х₁=7, х₂=-8 (не подходит). ⇒

АD=x=7 см, CD=7 см+1=8 см

Вокружность вписан четырехугольник со сторонами 8 и 15 см а угол между ними равен 60 градусам найдит

4,7(55 оценок)

Ответ:

mishanya2011198

15.03.2023

Так как известно отношение OD/OB=3/5, то можно обозначить OD=3x (OD=r - значит, 3х - искомый радиус), OB=5x, следовательно BD=8х. Также обозначим АС=а.

Площадь треугольника равна половине произведение его периметра на радиус вписанной окружности:
$S= \frac{1}{2} Pr\Rightarrow r= \frac{2S}{P}$

С другой стороны площадь можно найти как половина произведения основания на высоту:
$S= \frac{1}{2} \cdot AC\cdot BD$
Тогда выражение для радиуса вписанной окружности примет вид:
$r= \frac{AC\cdot BD}{P}$

Подставим в последнее выражения все ранее введенные обозначения и известные числовые данные:
$r=\frac{a\cdot 8x}{a+10+10}$
Зная, что r=3x, получим:
$3x=\frac{8ax}{a+20}
\\\
3=\frac{8a}{a+20}
\\\
8a=3a+60
\\\
5a=60
\\\
a=12
\\\
AC=12$

Рассмотрим треугольник АВD: AD есть половина АС, так как BD - высота (следовательно и медиана) равнобедренного треугольника. По теореме Пифагора получим:
$AB^2=( \frac{AC}{2} )^2+BD^2
\\\
10^2=6^2+(8x)^2
\\\
100=36+64x^2
\\
64=64x^2
\\\
x^2=1
\\\
x=1, \ x \neq -1$

Теперь можно найти радиус вписанной окружности:
$r=3x=3\cdot1=3$

ответ: 3

Дано: δabc, ab=bc, bd⊥ac, od/ob=3/5, ab=10. найти: r ( радиус вписанной окружности) решение: