1. sin <A = √ (1-cos² <A)
sin <A = √ (1-0,8²)
sin <A = 0,6
sin <A = BC / AB
0,6 = 6 / AB, AB = 10 см
по теоремі Піфагора: АС² = 10²-6²
АС = 8 см
РΔАВС = 6 + 10 + 8
РΔАВС = 24 см
2. 1 + tg² <A = 1 / cos² <A
1 + 0,75² = 1 / cos² <A
1,5625 = 1 / cos² <A
cos <A = 0,8
cos <A = AC / AB
0,8 = AC / 15
AB = 12 см
по теоремі Піфагора: ВС = √ (15²-12²), ВС = 9 см
РΔАВС = 15 + 12 + 13, Р = 40 см
3. cosA = √ (1-sin²A), cosA = 0,6
cosA = AC / AB
0,6 = 12 / AB, AB = 20 см
BC = √ ( 20²-12²), BC = 16 см
PΔABC = 20 + 12 + 16
PΔABC = 48 см
Объяснение:
Объяснение:
6)Узнаем периметр и площадь меньшего треугольника: p=3*а3=18√3
s=(a²√3)/4=(36*3√3)/4=27√3 кв. ед.
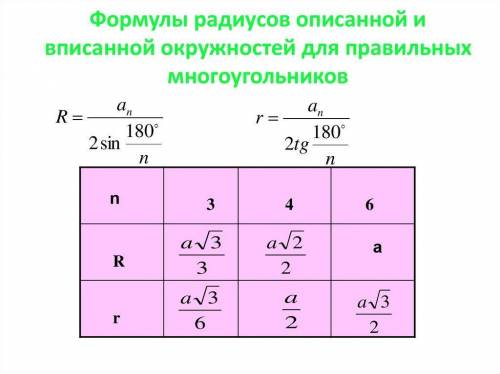
для маленького треугольника данная окружность описанная, поэтому ее радиус будет R=(a3√3)/3=(6√3*√3)/3=6
Для большего треугольника это окружность вписанная, поэтому R=(A√3)/6 => A=6R/√3=6*6/√3=36/√3=12√3
P=3A=12√3*3=36√3
S=(a²√3)/4=(144*3√3)/4=108√3 кв.ед.
9)p=4* 5√3=20√3
s=a²=(5√3)²=25*3=75 кв.ед
Так как у описанной вокруг меньшего квадрата окружности такой же радиус, что и у вписанной в больший кавдрат (ведь это одна и та же окружность), то можем их приравнять
R=(a√2)/2
r=A/2
(a√2)/2=A/2
A=2*(a√2)/2=a√2=5√3*√2=5√6
P=4A=4*5√6=20√6
S=A²=(5√6)²=25*6=150 кв.ед.
12) Для шестиугольника данная окружность описанная, а для квадрата--вписанная. Приравняем формулы для радиуса этой окружности
R=a6
r=a4/2
a6=a4/2=(4√2)/2=2√2
P4=4*a4=4*4√2=16√2
S4=(a4)²=(4√2)²=16*2=32 кв.ед.
я думаю новерное будет 6