|AC| = 10 см.
Объяснение:
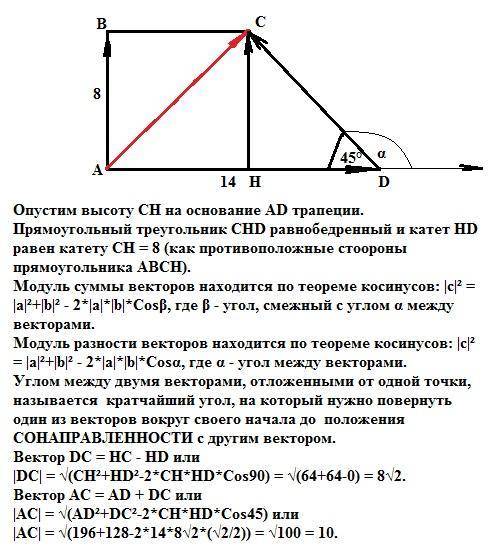
Опустим высоту СН на основание AD трапеции.
Прямоугольный треугольник СНD равнобедренный и катет HD равен катету СН = 8 (как противоположные стоороны прямоугольника АВСН).
Модуль суммы векторов находится по теореме косинусов: |c|² = |a|²+|b|² - 2*|a|*|b|*Cosβ, где β - угол, смежный с углом α между векторами.
Модуль разности векторов находится по теореме косинусов: |c|² = |a|²+|b|² - 2*|a|*|b|*Cosα, где α - угол между векторами.
Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения СОНАПРАВЛЕННОСТИ с другим вектором. Итак,
Вектор DC = НС - HD или
|DC| = √(CH²+HD²-2*CH*HD*Cos90) = √(64+64-0) = 8√2.
Вектор АС = AD + DC или
|AC| = √(AD²+DC²-2*CH*HD*Cos45) или
|AC| = √(196+128-2*14*8√2*(√2/2)) = √100 = 10.
ответ: Длина вектора (модуль) АС = 10 см.
Сторона AB=17 см
Диагональ AC=16
Найти диагональ BD
O - точка пересечения диагоналей ромба
Угол AOB - прямой, равен 90 градусов
AO=CO=16/2=8 см
Треугольник AOB прямоугольный
AB - гипотенуза
AO, BO - катеты
Сумма квадратов катетов равна квадрату гипотенузы
(теорема Пифагора)
AO^2 + BO^2 = AB^2
(^2 - в квадрате; 2-й степени)
8^2 + x^2 = 17^2
x^2 = 17^2 - 8^2
x^2 = 289 - 64
x^2 = 225
x = sqrt 225
(sqrt 225 - корень квадратный из 225)
x = 15
BO = 15 см
ВD = BO*2 = 15*2 = 30 см