Геометрия: Решите треугольние cde, угол с＝60 градусов сd＝8дм се＝5дм

Решите треугольние cde, угол с＝60 градусов сd＝8дм се＝5дм

👇

Увидеть ответ

Ответ:

sanyahit

27.10.2020

Решить треугольник - значит найти его недостающие элементы (стороны и углы).

По теореме косинусов DE = √(CD²+CE² - 2*CD*CE*Cos60) или

DE = √(64+25 - 2*8*5*1/2) = √49 = 7 дм.

По теореме синусов:

DE/Sin60=CD/SinE=CE/SinD. => SinD=CE*Sin60/DE = 5*√3/2*7 ≈0,618. SinE = CD*Sin60/DE = 8*√3/2*7 ≈ 0,9897.

Тогда по таблице <D ≈ 38°, a <E ≈ 82°.

ответ: DE=7дм, <D=38°, <E=82°

4,5(90 оценок)

Открыть все ответы

Ответ:

kashamovasha

27.10.2020

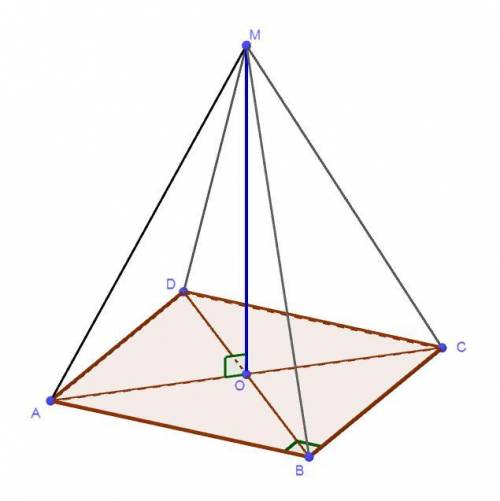
Точка пересечения диагоналей квадрата является центром квадрата. Т.к. из него проведена перпендикулярная прямая, значит расстояние от т. О до вершин квадрата будет одинаковое. Следовательно, нам нужно найти одно такое расстояние, чтобы знать все.

Стороны квадрата (а) равны. Диагонали у квадрата равные (d), и точк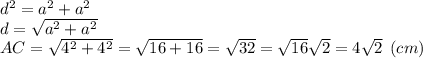 $d^2=a^2+a^2\\d=\sqrt{a^2+a^2} \\AC=\sqrt{4^2+4^2}=\sqrt{16+16}=\sqrt{32}=\sqrt{16}\sqrt{2}=4\sqrt{2} \:\: (cm)$ а пересечения делит их пополам.

Р-м ΔAOM:

∠O = 90°, AO — половина диагонали, OM — перпендикуляр к плоскости квадрата. АМ — наклонная.

AO = d/2

Ищем, чему равна диагональ квадрата:

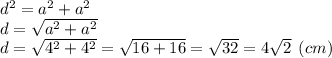
$d^2=a^2+a^2\\d=\sqrt{a^2+a^2} \\d=\sqrt{4^2+4^2}=\sqrt{16+16} =\sqrt{32}= 4\sqrt{2} \:\:(cm)$

AO = (4√2)/2 = 2√2 см

Теперь можем найти длину отрезка AM

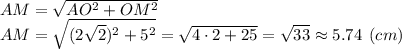
$AM=\sqrt{AO^2+OM^2} \\AM=\sqrt{(2\sqrt{2})^2+5^2}=\sqrt{4\cdot 2+25} =\sqrt{33} \approx 5.74 \:\: (cm)$

ответ: Расстояние равно √33 см, или приблизительно 5,74 см.

Через точку О пересечения диагоналей квадрата со стороной 4 см проведена прямая OM перпендикулярная

4,7(37 оценок)

Ответ:

кастусь

27.10.2020

1. Дано: угол 2 = угол 1 + 34°;
Найти: угол 3.
Решение:
Угол 3 и угол 1 - соотвественные углы при параллельных прямых a и b и секущей c. Следовательно, угол 3 = углу 1.
Углы 1 и 2 - односторонние при параллельных прямых a и b и секущей c⇒ угол 1 + угол 2 = 180°. Но, по условию, угол 2 = угол 1 + 34°. Подставим это выражение:
угол 1 + угол 1 + 34° = 180°.
Отсюда угол 1 = 73°.
Значит, угол 3 = 73°.
ответ: 73°.

2. Дано: ΔАВС, угол С = 90°, CD || AB, угол DCB = 37°.
Найти: угол А, угол В.
Рисунок к задаче - в приложении к ответу.
Решение:
Угол DCB и угол B - накрест лежащие углы при параллельных прямых AB и DC и секущей BC ⇒ угол DCB = углу B.
Т.к. угол DCB = 37°, то угол B = 37°.
Угол A + угол В + угол ACB = 180° (по теореме о сумме углов треугольника), следовательно, угол A = 180° - угол В - угол ACB.
Угол А = 180° - 90° - 37° = 53°.
ответ: угол А = 53°, угол В = 37°.

4,4(60 оценок)

Это интересно:

Образование

21.07.2020

Из разных городов, расстояние между которыми 600 км...

Образование

02.06.2023

В треугольнике АВС точка D на стороне АВ...

Образование

27.04.2022

Первые 300 км автомобиль ехал со скоростью 60 км/час...

Образование