Начертили ромб ABCD.
Рассмотрим ΔAOD:
АО=2
AD=√13
OD²=AD²-AO²
OD²=13-4
OD=3
BD=6
Sabcd=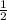
×d1×d2
Sabcd= 12
Точка, назовём её С(х;у;z) равноудалена от точек А(1,2,3) и В(-3,3,2).
Это означает, что расстояние АС равно расстоянию ВС.
Точка С принадлежит оси ОХ, значит её координаты равны (х;0;0)
Расстояние между точками можно определить по формуле:
sqr((x2-x1)^2+(y2-y1)^2+(z1-z2)^2), значит
sqr((х-1)^2+(0-2)^2+(0-3)^2)=sqr((x+3)^2+(0-3)^2+(0-2)^2)
(x-1)^2+4+9=(x+3)^2+9+4
(x-1)^2=(x+3)^2
x^2-2x+1=x^2+6x+9
-8x=8
x=-1
Итак, искомая точка, равноудалённая от А и В имеет координаты
С(-1;0;0)
Точка, назовём её С(х;у;z) равноудалена от точек А(1,2,3) и В(-3,3,2).
Это означает, что расстояние АС равно расстоянию ВС.
Точка С принадлежит оси ОХ, значит её координаты равны (х;0;0)
Расстояние между точками можно определить по формуле:
sqr((x2-x1)^2+(y2-y1)^2+(z1-z2)^2), значит
sqr((х-1)^2+(0-2)^2+(0-3)^2)=sqr((x+3)^2+(0-3)^2+(0-2)^2)
(x-1)^2+4+9=(x+3)^2+9+4
(x-1)^2=(x+3)^2
x^2-2x+1=x^2+6x+9
-8x=8
x=-1
Итак, искомая точка, равноудалённая от А и В имеет координаты
С(-1;0;0)
а = √13 - длина стороны ромба
d = 4 - меньшая диагональ
Поскольку диагонали ромба взаимно перпендикулярны, то найдём вторую диагональ D по теореме Пифагора
D = 2√(a² - (0,5d)²) = 2 · √(13 - 4) = 6
Площадь ромба S = 0.5·d · D = 0.5 · 4 · 6 = 12