Question

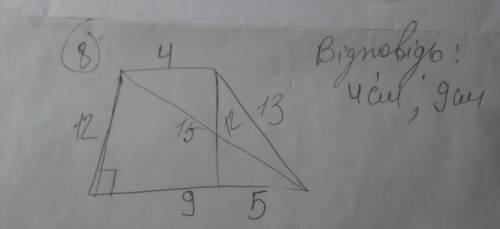
7. в равнобедренном треугольнике авс (основание ас) боковая сторона равна 17см, а высота ак равна 8см. найдите длины средних линий данного треугольника.. 8. в прямоугольной трапеции боковые стороны 12см и 13см, а большая диагональ 15см. найдите основания трапеции.

Answer 1

Answer 2

7. Для начала нам нужно понять, что такое средняя линия в равнобедренном треугольнике. Средняя линия - это линия, соединяющая середины двух сторон треугольника, которые не являются его основанием.

Итак, у нас есть равнобедренный треугольник АВС, где АС - основание, а ВС = 17 см - боковая сторона, а ВК = 8 см - высота.

Мы знаем, что высота разделяет основание на две равные части. То есть АК = КС. Это происходит из свойств равнобедренных треугольников.

Теперь нам нужно найти середину ВК. Для этого мы можем использовать свойство серединной линии равнобедренного треугольника, которое гласит, что серединная линия равна половине основания.

Значит, ВК = (1/2) * 17см = 8,5см.

Теперь мы можем найти АВ - другую серединную линию. Используем снова свойство серединной линии, которое гласит, что серединная линия равна полусумме основания и боковой стороны треугольника.

АВ = (17см + 8,5см) / 2 = 25,5см / 2 = 12,75см.

Таким образом, длины средних линий данного треугольника равны 8,5см и 12,75см.

8. Данная задача также использует свойство прямоугольной трапеции, что диагонали она делит пополам.

У нас есть прямоугольная трапеция ABCD, где AB и CD - боковые стороны, AD и BC - основания, а AC - большая диагональ.

Мы знаем, что AC делит BC пополам, значит BC = 15см / 2 = 7,5см.

Теперь мы можем использовать теорему Пифагора, чтобы найти длину основания AD. Вспомним, что в прямоугольной трапеции сумма квадратов оснований равна квадрату диагонали.

AD^2 + BC^2 = AC^2
AD^2 + 7,5см^2 = 15см^2
AD^2 + 56,25см^2 = 225см^2
AD^2 = 225см^2 - 56,25см^2
AD^2 = 168,75см^2

Теперь возведем обе части уравнения в квадратный корень, чтобы найти AD.

AD = √(168,75см^2) ≈ 12,99см

Таким образом, длины оснований трапеции составляют около 7,5см и 12,99см.