|CM| = 5.
Объяснение:
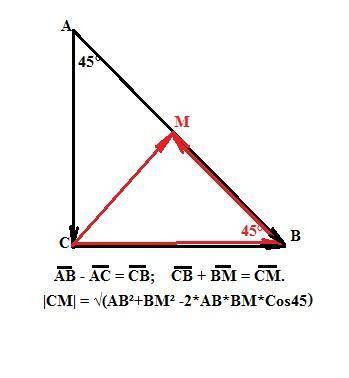
Речь идет о векторах. По правилу вычитания и сложения векторов имеем:
АВ - АС = СВ; СВ + ВМ = СМ.
|CM| = 5 см , так как это медиана из прямого угла.
Или так:
Треугольник АВС равнобедренный, следовательно
<BAC = <ABC = 45°.
АМ = 5 см, так как СМ - медиана. В треугольнике АМС
Cos(<MAC) = AM/AC = Cos45° =>
AC = AM/Cos45 = 5/(√2/2) = 5√2.
Разность векторов AB - AC = CB (по правилу разности векторов)
|CB| = √(AB²+AC² - 2*AB*BC*Cos45) или
|CB| = √(100+50-2*10*5√2*√2/2) =√50=5√2.
Cумма векторов СВ +ВМ = СМ (по правилу сложения векторов).
|CM| = √(CB²+BM² - 2*CB*BM*Cos45) = √(50+25-50) = 5.
Щоб знайти площу трикутника, ми можемо скористатися формулою площі трикутника:
Площа = (1/2) * a * b * sin(C),
де a і b - довжини сторін трикутника, а C - кут між цими сторонами.
У цьому випадку, a = 8 см, b = 5 см і C = 45°.
Підставляючи ці значення в формулу, отримуємо:
Площа = (1/2) * 8 см * 5 см * sin(45°).
Для обчислення sin(45°) ми можемо скористатися значенням sin(45°) = 1/√2 = √2/2.
Підставляючи це значення, отримуємо:
Площа = (1/2) * 8 см * 5 см * (√2/2) = 20√2 см².
Отже, площа трикутника дорівнює 20√2 см².
образует с боковым РЕБРОМ угол y.
b/2=R*cos(y)
Rш=b/[2*cos(y)]
Vш=4/3*pi*Rш^3=4/3*pi*(b/[2*cos(y)])^3