Отрезки АB DC лежат на параллельных прямых, а отрезки А
1.Угол АОD паралелен углу ВОС,следовательно он равен 23 градуса.Угол АОВ равен 180 - 23=157 градусов.Угол DOC паралелен углу АОВ,,следовательно равен 157 градусов.
2.Углы BOF AOF равны по стороне и углу,следовательно 32+32=64 градуса.Угол ВОС равен 180-64=116 градусов.
3.Угол АОВ параллелен DOE,следовательно они равны.Угол FOA и COD параллельны. Угол FOC равен 25+55=80 градусов.Угол FOE равен 180 -80=100 градусов.
4.∠AOD + ∠AOC + ∠BOD + ∠BOC = 360° ∠AOD + ∠AOC + ∠BOC = 210 °, значит ∠BOD = 360° - 210° = 150° ∠AOD = 180° - ∠BOD = 180° - 150° = 30° так как это смежные углы.
Площадь полной поверхности призмы - это сумма площадей двух оснований (ромбов) и четырех боковых граней (прямоугольников со сторонами, равными высоте и стороне основания призмы). В ромбе диагонали взаимно перпендикулярны и делятся точкой пересечения пополам. => Сторона основания (ромба) по Пифагору равна
а = √((D/2)²+(d/2)²) или а = √(4²+3²) = 5см.
Площадь боковой грани равна Sг= 5*10 = 50см²
Площадь основания равна (1/2)*D*d = 6*8/2=24см².
Площадь полной поверхности призмы равна S=2*24+4*50 = 248 см²
ответ: S=248 см²
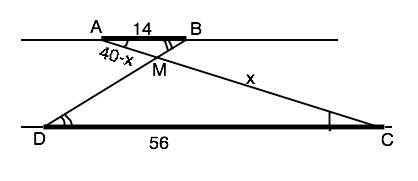
Отрезки АВ и DC лежат на параллельных прямых, следовательно, АВ║DC, АС и ВD – секущие. Из свойства углов при пересечении параллельных прямых секущей следует равенство накрестлежащих углов: ∠ВАС=∠АСD и ∠АВD=∠BDC. Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны. Из подобия ∆ АВМ и ∆ CDM следует отношение МС:МА=DС:AB. Примем МС=х, тогда МА=40-х. Составим пропорцию: 56:14=х:(40-х) ⇒ 4:1=х:(40-х) ⇒ х=160-4х ⇒ 5х=160, МС=х=32