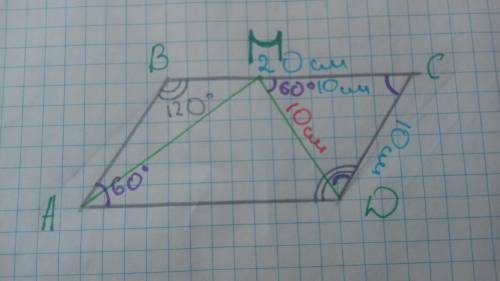
а) AB=CD=10см
BC=AD=20см
б) ABC=CDA=120 градусов
BAD=BCD=60 градусов
Объяснение:
когда мы провели биссектрису MD у нас получился равносторонний треугольник у которого все стороны одинаковые: CD=DM=MC=10см и углы равняются 60 градусам: DMC=MCD=CDM=60 градусам. теперь нам известно, что стороны CD=BA=10см по скольку эти стороны параллельные. в суме эти два угла дают 20 см. чтобы найт другую сторону параллелограмма нам надо от периметра отнять 20 см и поделить на 2: (60-20):2=20 - сторона BC (AD) .углы MCD=BAD=60 градусам. чтобы найти углы ABC и BCD мы от 180 градусов отнимаем угол ABC (BCD) (потому что углы на одной стороне параллелограмма равны 180 градусам): ABC (BCD)= 180-60=120 градусов
2.180-70=110 110:2=55 (градусов)
3.АВСД - пар-м. ВД перпенд АД. ВД = АВ/2Тогда треугольник АВД - прямоугольный и катет ВД - вдвое меньше гипотенузы АВ. Значит угол ВАД = 30 гр.Тупой угол пар-мма тогда равен 180 - 30 = 150 гр.Отсюда ответ: 30; 150; 30; 150 град.
4.Задача решается только при условии, что трапеция равнобочная, т.е АВ = СД. поскольку угол Д-60гр., то угол САД равен 30 градусов (180-90-60), известно, что катет лежащий против угла в 30 гр,равен половине гипотенузы, т.е АД. Далее, расмотрим треугольник АВС- он равносторонний, поскольку углы САД и ВСА равны, и углы САД и САВ тоже равны, поскольку АС- биссектриса. Отсюда ясно, что верхнее основание и боковые стороны равны- обозначим их Х А нижнее основание будет 2Х. Тогда систавин и решим уравнение 35= Х+Х+Х+2Х= 5Х Х= 7