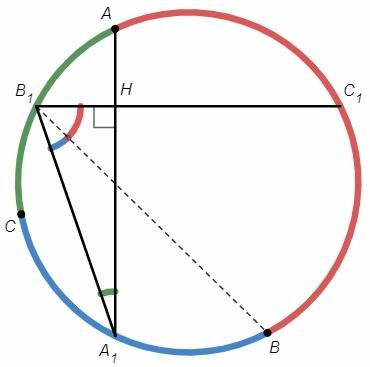
Вершины △ABC разбивают описанную окружность на три дуги. Биссектрисы углов треугольника делят эти дуги пополам (два равных вписанных угла опираются на равные дуги), точки A1, B1, C1 - середины дуг.
Вписанные углы ∠BB1C1, ∠BB1A1, ∠A1 опираются на половины дуг AB, BC, AC, следовательно сумма вписанных углов равна четверти окружности, 90.
∠BB1C1+∠BB1A1+∠A1 =∪AB/4+∪BC/4+∪AC/4 =360/4 =90
AA1 и B1C1 пересекаются в точке H. В △A1B1H сумма углов ∠A1 и ∠B1 равна 90, треугольник прямоугольный, AA1 и B1C1 пересекаются под прямым углом.
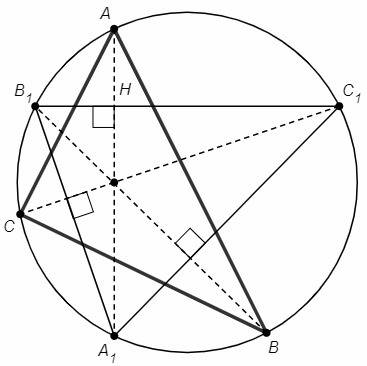
Аналогично BB1⊥A1C1, CC1⊥A1B1. Биссектрисы △ABC являются высотами △A1B1C1. Центр вписанной окружности (пересечение биссектрис) △ABC является ортоцентром (пересечением высот) △A1B1C1.
Периметр параллелограмма больше одной стороны на 29 см и больше другой на 22 см. Найдите наименьшую сторону параллелограмма.
Объяснение:
В параллелограмме АВСД :
АВ=СД , ВС=АД, Р=29+АВ, Р=22+АД.
Т.к. Р=29+АВ, то АВ=Р-29,
АВ=2АВ+2АД-29,
29=АВ+2АД или АВ=29-2АД (*).
Т.к. Р=22+АД, то АД=Р-22,
АД=2АВ+2АД-22,
22=2АВ+АД (**).
Подставим (*) в (**) получим
22=2(29-2АД)+АД,
22=58-4АД+АД ,
3АД=58-22
АД=36:3
АД=12 см. Тогда АВ=29-2*12=5 (см)
ответ. наименьшая сторона параллелограмма 5 см.
Найдем площадь основания параллелепипеда S=аbsin60°=6·6·√3/2=18√3.
Рассмотрим треугольник, сторонами которого являются: меньшая диагональ нижнего основания параллелепипеда, меньшая диагональ параллелепипеда и высота параллелепипеда.
Этот треугольник прямоугольный с острыми углами по 45°. Значит его катеты равны.
Меньшая диагональ основания (ромба) делит ромб на два равносторонних треугольника, значит меньшая диагональ равна 6 см и высота также равна 6 см.
V=Sh=6·18√3=108√3 cм³.
ответ: 108√3 см³.
Я новичок так что хз правильно или нееет..
////////////////////////////////////////////////////