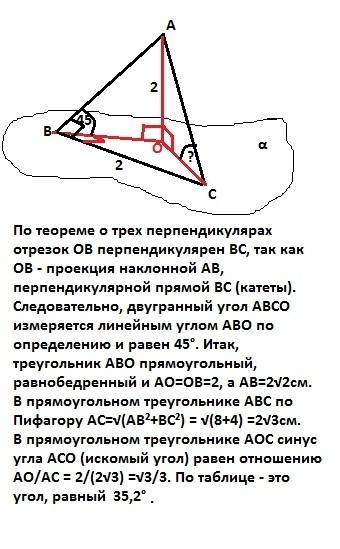
По теореме о трех перпендикулярах отрезок ОВ - проекция наклонной АВ, перпендикулярной прямой ВС (катеты). Следовательно, двугранный угол АВСО измеряется линейным углом АВО по определению и равен 45° (дано). Треугольник АВО прямоугольный и равнобедренный. Катеты АО=ОВ=2см, а гипотенуза АВ=2√2 см. В прямоугольном треугольнике АВС по Пифагору АС=√(АВ² +ВС²) = √(8+4) = 2√3см. В прямоугольном треугольнике АОС синус угла АСО (искомый угол, так как это угол между наклонной АС и плоскостью α по определению) равен отношению АО/АС = 2/(2√3) = √3/3. По таблице - это угол, равный 35,2°.
ответ: 35,2°.
даю правильный ответ
такое геометрическое место - это 4 точки, соотвестствующие возможному положению вершины прямоугольного треугольника со сторонами-катетами 6 и 8 при заданном положении гипотенузы 10. Никаких других вариантов нет. Все эти точки легко найти, проведя окружности радиусом 6 и 8 с центрами в разных концах отрезка. Точки пересечения и будут ГМТ. Все эти точки расположены в вершинах прямоугольника, симметричного относительно отрезка и линии проходящей через его середину. Сторона этого прямоугольника, перпендикулярная отрезку, равна удвоенной высоте такого треугольника . h*10 = 6*8, h = 4,8, сторона 9,6. Вторая сторона этого прямоугольника находится так. Обозначим за х больший отрезок, который высота отсекает от гипотенузы, тогда х/8 = 8/10, x = 6,4. расстояние от вершины до медиатриссы равно х - 10/2 = 1,4, ну, а сторона прямоугольника - 2,8
Если выбрать систему координат так, что ось Х идет вдоль отрезка, а О расположен в центре, то координаты точек таковы
(1,4;4,8),(-1,4;4,8),(1,4;-4,8),(-1,4;-4,8) это и есть ГМТ.
: