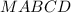 - правильная четырехугольная пирамида, около которой описан конус
- правильная четырехугольная пирамида, около которой описан конус 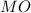 ⊥
⊥ 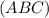
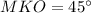
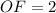 см
см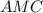 - осевое сечение конуса, где
- осевое сечение конуса, где 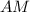 и
и 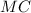 - образующие конуса
- образующие конуса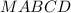 - правильная четырехугольная пирамида,
- правильная четырехугольная пирамида, 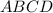
 ∩
∩ 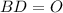
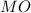 ⊥
⊥ 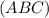
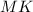 ⊥
⊥ 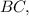 тогда
тогда 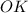 ⊥
⊥ 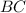 и
и 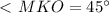 как линейный угол двугранного угла
как линейный угол двугранного угла  - центр окружности, описанной около квадрата
- центр окружности, описанной около квадрата  , т. е.
, т. е. 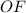 ⊥
⊥ 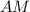
 тогда
тогда 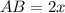
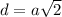 , где
, где 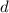 - диагональ квадрата,
- диагональ квадрата,  - сторона квадрата
- сторона квадрата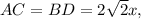 ( как диагонали квадрата)
( как диагонали квадрата)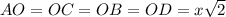
 - прямоугольный, равнобедренный, следовательно
- прямоугольный, равнобедренный, следовательно 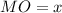
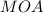 - прямоугольный
- прямоугольный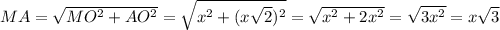
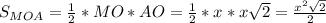 ,
,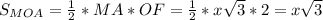
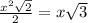
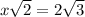
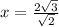
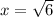
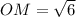 см
см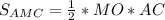
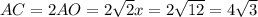 см
см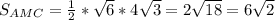 (см ²)
(см ²)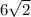 см²
см²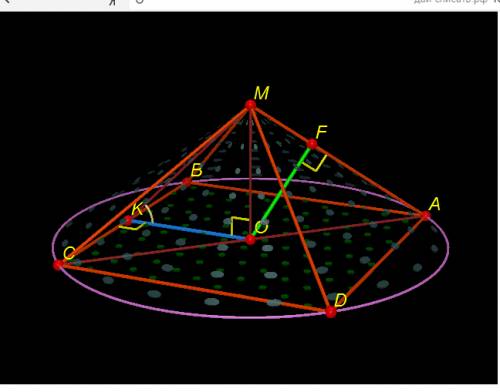
В четырёхугольнике диагонали равны 12 и 8 и пересекаются под углом в 30°. Найдите площадь четырёхугольника.
=====================================
Площадь любого произвольного четырёхугольника вычисляется по формуле:S = d₁ • d₂ • sinα / 2где d₁ , d₂ - длины диагоналей данного четырёхугольника, α - угол между диагоналями
S = 12 • 8 • sin30° / 2 = 12 • 8 • 0,5 / 2 = 24ОТВЕТ: 24