ответ: 1) меньшие по 48°, большие по 132°.
2) меньшие по 40°, большие по 140°
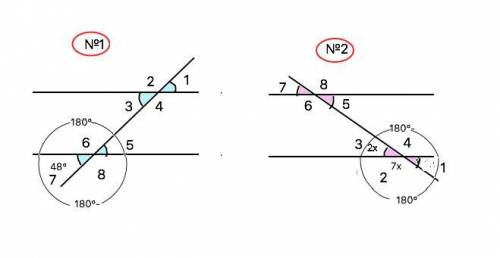
Объяснение: При пересечении двух параллельных прямых секущей образуется пары равных углов:
соответственные (2 и 6, 1 и 5, 3 и 7, 4 и 8).
накрестлежащие: (3 и 5, 4 и 6 - внутренние ), (2 и 8, 1 и 7 - внешние). кроме того, равны и пары вертикальных углов.
1) Как известно, сумма смежных углов равна 180°. Поэтому углы, смежные углу, равному 48°, равны 180°-48°=132°
На рисунке 1 все мéньшие углы, окрашенные голубым, равны 48°. все бóльшие - 132°
2) На рисунке 2 смежные углы 2 и 3 относятся как 2:7. Т.е. развернутый угол делится на 2+7=9 частей. Каждая часть равна 180°:9=20°. Поэтому все мéньшие углы равны 2•20°=40°, бóльшие 7•20°=140°.
квадрат-фигура на плоскости состоящая из четырех равных пересекающихся отрезков- образующих четыре угла-равных 90 градусов.соединение противоположных точек пересечения прямой называется диагональю квадрата.-она образует таким образом 2 прямоугольных равнобедренных треугольника. прямоугольный треугольник имеет три стороны-две из них-прилежащие к прямому углу(90 градусов)-называются "катет"-а линия -соединяющая концы этих катетов-называется -"гипотенуза". итак-для решения задачи нахождения любой из сторон прямоугольного тр-ка обратимся к теореме Пифагора.
которая гласит- квадрат размера гипотенузы прямоугольного тр-ка= сумме размеров катетов возведенных в квадрат.упрощенно(квадрат гипотенузы=сумме квадратов катетов.)
площадь квадрата вычисляется=произведением его сторон т.о. для вычисления площади квадрата-необходимо найти(вычислить) сторону квадрата или(в нашем случае-катет прямоугольного тр-ка с гипотенузой-Д.)пользуясь теоремой Пифагора составим равенство-
Д²=Х² +Х². Д²=2Х². Х²=Д²/2. ГДЕ Х-СТОРОНА КВАДРАТА!
ОТВЕТ S КВАДРАТА=Д²/2