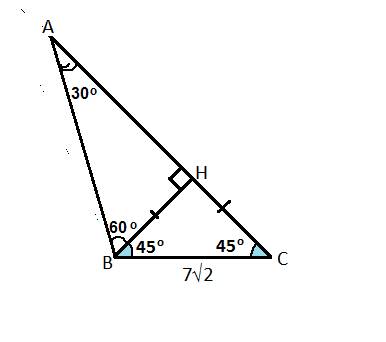
Диаметр окружности, описанной около прямоугольного треугольника, рувен длине гипотенузы этого треугольника.
L=πD=16π.
Объяснение:
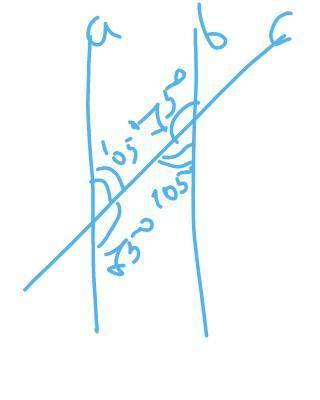
Есть такое правило: накрест лежащие углы равны. Т.е. если мысленно провести две линии от двух разных углов к двум другим так, что они образуют крест, углы, на концах этих линий, будут равны. Тобишь угол 2=75(т.к. он накрест лежащий). Угол 2(или три -- они всё равно равны) смежен с соседним(составляют вместе развёрнутый угол). Соответственно для того, чтобы вычислить углы 1 и 4 нужен из 180(развернутого угла) вычесть угол 2 или 3(75 градусов). Мы получаем 105. Следующим пунктом можно проделать то же самое с неизвестным углом, либо вычислить его по правилу накрест лежащего угла(с 1 или 4 в зависимости от того, какой вы находили).
Если мой ответ показался Вам полным и доступным , выберете его лучшим.
По свой описанной окружности, её радиус равен половине длины гипотенузы. Длина окружности = 2пr = 2*8*п = 16п или ~50,24